RH铝脱氧后夹杂物碰撞聚合去除的数学模型

郝赳赳

doi:10.7513/j.issn.1004-7638.2022.01.019

RH铝脱氧后夹杂物碰撞聚合去除的数学模型

doi: 10.7513/j.issn.1004-7638.2022.01.019

郝赳赳^{1, 2,}

1.
山西工程职业学院冶金与环境工程系, 山西太原 030009
2.
北京科技大学冶金与生态学院, 北京 100083

基金项目: 2019年度山西省高等学校科技创新项目(2019L0995)

详细信息

作者简介:
郝赳赳（1982—），女，博士，山西工程职业学院副教授，研究方向：钢铁冶金，E-mail：731536257@qq.com

中图分类号: TF769.4
计量
- 文章访问数: 74
- HTML全文浏览量: 9
- PDF下载量: 32
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-19
- 网络出版日期: 2022-04-24
- 刊出日期: 2022-02-28

Numerical model of collision aggregation and remove of inclusions after aluminum deoxidization in RH reactor

Hao Jiujiu^{1, 2
,}

1.
Department of Metallurgy and Environmental Engineering, Shanxi Engineering Vocational College, Taiyuan 030009, Shanxi, China
2.
School of Metallurgical and Ecological Engineering, University of Science and Technology, Beijing 100083, China

摘要

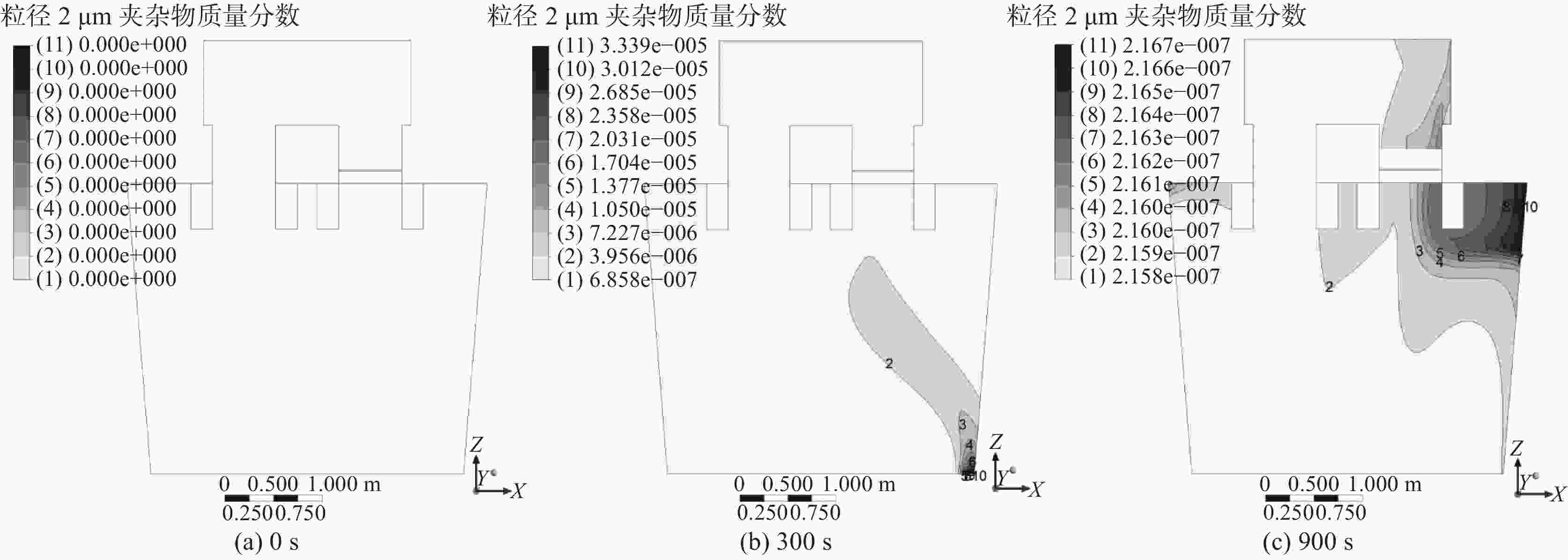
摘要: 在夹杂物碰撞经典聚合模型的基础上，使用了指数级增长的夹杂物分组方式，建立RH铝氧反应生成夹杂物、夹杂物碰撞聚合和夹杂物去除过程的数学模型，从而对RH冶炼过程夹杂物的质量分数及分布进行预测。得到结论如下：模拟结果与文献给出数据有很好的吻合度，模型真实可靠。夹杂物质量分数随着金属铝的加入而快速增加，循环300 s后，夹杂物的总质量分数从最开始的0升至0.065%左右，夹杂物质量分数达到最大值，继而在上浮、壁面吸附和顶渣吸附的作用下去除。经过900 s左右的钢液循环后，夹杂物的总质量分数降至0.01%左右，其整体去除率在84.6%左右，说明RH循环对夹杂物有很好的去除作用。加铝后900 s，2 μm和50.8 μm的夹杂物质量分数的最大值分别为0.00002%和0.0078%。
- RH /
- 铝氧反应 /
- 夹杂物 /
- 碰撞聚合 /
- 数学模型
Abstract: Based on the classical model of collision aggregation of inclusions, the growth mode of exponential increase of inclusions is used to establish the numerical model of reaction of aluminum and oxygen, collision and aggregation of inclusions, remove of inclusions, for the purpose of predicating the mass fraction and distribution of inclusions during the process of RH. The simulated results are found out good agreement previous findings from the developed model, the mass fraction of inclusions is sharply increasing with the plunge of aluminum. The mass fraction of inclusions increases from 0 to 0.0065% after 300 s circulation. Then the mass fraction reaches the maximum value. Afterwards the inclusions begin to remove because of the float and adsorption by the wall and the top slag of RH. The mass fraction of inclusions decreases to about 0.01% after 900 s circulation. The percentage of inclusions removal is 84.6%. The circulation has effectively removed the inclusions in RH. After 900 s circulation the maximum mass fractions of inclusions of diameter 2 μm and 50.8 μm are 0.000 02% and 0.0078% respectively.
- RH /
- reaction of aluminum and oxygen /
- inclusions /
- collision aggregation /
- numerical model

HTML全文

图 1 RH夹杂物质量分数随时间变化曲线

Figure 1. The curve of mass fraction of inclusions in RH with time

下载: 全尺寸图片幻灯片

图 2 不同时刻粒径2 μm夹杂物质量分数分布云图

Figure 2. The contour of mass fraction of inclusions of diameter 2 μm at different time

下载: 全尺寸图片幻灯片

图 3 不同时刻粒径50.8 μm夹杂物质量分数分布云图

Figure 3. The contour of mass fraction of inclusions of diameter 50.8 μm at different time

下载: 全尺寸图片幻灯片

表 1 模拟参数及其数值

Table 1. Parameters and values of simulation

提升气体流量/
（m³·h⁻¹）钢液重量/
t 循环时间/
s 初始溶解氧浓度/
% 加入金属铝质量/
kg

96 210 900 0.0658 336

下载: 导出CSV

参考文献(20)

[1]	陈固军. RH真空精炼过程流体流动和夹杂物行为的数值模拟[D]. 重庆: 重庆大学, 2017. Chen Gujun. Numerical simulation of fluid flow and inclusion behavior in RH vacuum refining process[D]. Chongqing: Chongqing University, 2017.
[2]	王耀. 基于分形理论模拟钢中夹杂物上浮及碰撞凝聚规律的研究[D]. 北京: 北京科技大学, 2015. Wang Yao. Research of simulation inclusion floating, collision and aggregation law in molten steel based on fractal theory[D]. Beijing: University of Science and Technology Beijing, 2015.
[3]	段豪剑. 钢液中非金属夹杂物相关界面现象的基础研究[D]. 北京: 北京科技大学, 2018. Duan Haojian. Fundamental on interfacial phenomena of non-metallic inclusions in molten steel[D]. Beijing: University of Science and Technology Beijing, 2018.
[4]	Smoluchowski M. Versuch einer mathematischen theorie der koagulationskinetik kolloider Lösungen[J]. Zeitschrift Für Physikalische Chemie, 1917,92(3):129−168.
[5]	张建, 李海键. 气体搅拌条件下基于计算流体动力学的钢液中夹杂物的长大与去除模型[C]. 北京: 中国金属学会, 2003. Zhang Jian, Li Haijian. A CFD-based model for growth and removal of inclusions in molten steel under gas-stirring conditions[C]. Beijing: The Chinese Society for Metals, 2003.
[6]	Wang L T, Zhang Q Y, Peng S H, et al. Mathematical model for growth and removal of inclusion in a multi-tuyere ladle during gas-stirring[J]. ISIJ International, 2005,45(3):331−337. doi: 10.2355/isijinternational.45.331
[7]	Zhang J, Lee H G. Numerical modeling of nucleation and growth of inclusions in molten steel based on mean processing parameters[J]. ISIJ International, 2004,44(10):1629−1638. doi: 10.2355/isijinternational.44.1629
[8]	Zhang L F, Pluschkell W. Nucleation and growth kinetics of inclusions during liquid steel deoxidation[J]. Ironmaking and Steelmaking, 2003,30(2):106−110. doi: 10.1179/030192303225001766
[9]	Lindborg U, Torssell K. A collision model for the growth and separation of deoxidation products[J]. Transactions of the Metallurgical Society of AIME, 1968,242(1):94−96.
[10]	Pesteanu O. Short contribution to the mathematical modeling of coagulation effect on entrapped inclusion concentration in continuously cast steel[J]. ISIJ International, 2006,46(2):339−340. doi: 10.2355/isijinternational.46.339
[11]	Gelbard F, Tambour Y, Seinfeld J H. Sectional representations for simulating aerosol dynamics[J]. Journal of Collioid and Interface Science, 1980,76(2):541−556. doi: 10.1016/0021-9797(80)90394-X
[12]	Naaoka T, Taniguchi S, Matsumoto K, et al. Particle-size-grouping method of inclusion agglomeration and its application to water model experiments[J]. ISIJ International, 2001,41(10):1103−1111. doi: 10.2355/isijinternational.41.1103
[13]	Yamaguchi K, Kishimoto Y, Sakuraya T, et al. Effect of refining conditions for ultra low carbon steel on decarburization in RH degasser[J]. ISIJ International, 1992,32(1):126−135. doi: 10.2355/isijinternational.32.126
[14]	Takahashi M, Matsumoto H, Saito T. Mechanism of decarburization in RH degasser[J]. ISIJ International, 1995,35(12):1452−1458. doi: 10.2355/isijinternational.35.1452
[15]	Geng Dianqiao, Lei Hong, He Jicheng. Effect of different technological factors on inclusion removal in RH degasser[J]. Iron & Steel, 2009,44(10):26−30. (耿佃桥, 雷洪, 赫冀成. 不同工艺因素对RH精炼夹杂物去除过程的影响[J]. 钢铁, 2009,44(10):26−30. doi: 10.3321/j.issn:0449-749X.2009.10.007
[16]	Zhao Xinyu, Zhang Jiongming, Luo Yanzhao et al. Mathematical model of decarburization processes in RH refining for ultra-low carbon steel[J]. Journal of University of Science and Technology Beijing, 2012,34(8):876−882. (赵新宇, 张炯明, 罗衍昭, 等. 超低碳钢RH冶炼脱碳过程的数学模型[J]. 北京科技大学学报, 2012,34(8):876−882.
[17]	Friedlander S K, Wang C S. The self-preserving particle size distribution for coagulation by brownian motion[J]. Journal of Colloid and Interface Science, 1966,22(2):126−132. doi: 10.1016/0021-9797(66)90073-7
[18]	Saffman P G, Turne J Sr. On the collision of drops in turbulent clouds[J]. Journal of Fluid Mechanics, 1956,1(8):15−16.
[19]	Geng Dianqiao, Lei Hong, He Jicheng. Three-dimensional numerical simulation of coalescence and removal of inclusions in RH degasser[J]. Journal of Iron and Steel Research, 2009,21(12):10−13. (耿佃桥, 雷洪, 赫冀成. RH装置内夹杂物聚合与去除的三维数值模拟[J]. 钢铁研究学报, 2009,21(12):10−13.
[20]	Miki Y, Thomas B G, Denissov A, et al. Model of inclusion removal during RH degassing of steel[J]. Iron and Steelmaker, 1997,24(8):31−38.