Effects of mean load and load amplitude on biaxial dwell fatigue behavior of commercial pure titanium
-
摘要: 通过室温双轴保载疲劳试验,研究了不同平均载荷及载荷幅值对工业纯钛双轴保载疲劳行为的影响。结果表明,在相同保载时间下,平均应变及应变速率随着平均载荷和载荷幅值的升高而逐渐增大。当载荷幅值一定时,蠕变应变随着平均载荷的增大而增大,当平均载荷一定时,蠕变应变随着载荷幅值的增大反而减小。分析双轴棘轮与蠕变应变之间交互作用时,发现两者始终相互制约。断口分析表明,随着平均载荷和载荷幅值的增大,疲劳条带特征逐渐消失,韧窝及撕裂棱数量显著增加,断口呈现韧性失效特征。随着平均载荷或载荷幅值的增加,等效应变幅值增加,疲劳寿命逐渐降低。与平均载荷的影响相比,疲劳寿命对载荷幅值的变化更加敏感。分别利用最大主应变、最大剪应变、Mises等效应变、最大主应力及SWT模型进行双轴保载疲劳寿命预测,其中SWT模型预测精度最高。Abstract: Based on biaxial dwell fatigue tests at room temperature, effects of different mean loads and load amplitudes on the biaxial dwell fatigue behavior of commercial pure titanium were studied. The results show that the mean strain and strain rate increase with the increase of mean load and load amplitude under the same dwell time. When the load amplitude remains constant, the creep strain increases with the increase of the mean load. However, when the mean load remains constant, the creep strain decreases with the increase of the load amplitude. By analyzing the interaction between biaxial ratcheting and creep strain, it is found that ratcheting strain and creep strain are always restricted by each other. Fracture surface analysis shows that with the increase of mean load and load amplitude, the fatigue strip characteristics disappear gradually, and the number of dimples and tearing ridges significantly increases, exhibiting ductile failure mode. Meanwhile, with the increase of mean load or load amplitude, equivalent strain amplitude is increased, leading to the decrease of fatigue life. Compared with the effect of mean load, fatigue life is more sensitive to the variation of load amplitude. Maximum principal strain, maximum shear strain, Mises equivalent strain, maximum principal stress and SWT models are used to perform biaxial dwell fatigue life prediction, among them SWT model has the highest prediction accuracy.
-
Key words:
- commercial pure titanium /
- asymmetric load /
- biaxial dwell fatigue /
- life prediction
-
表 1 TA2在不同平均载荷及载荷幅值下的双轴保载疲劳试验方案
Table 1. Biaxial dwell fatigue test scheme of TA2 under different average loads and load amplitudes
编号 Fm/N Fa/N 半寿命周次 Nf Δεx/% Δεν/% ΔεZ/% Δεeq/% 1 1700 1200 0.448 0.354 -0.802 0.8038 6013 2 1800 1200 0.413 0.392 −0.805 0.8051 4420 3 1 900 1200 0.431 0.405 −0.836 0.8361 570 4 1700 1300 0.403 0.415 −0.818 0.8180 2638 5 1800 1300 0.435 0.407 −0.842 0.8422 1484 6 1 900 1300 0.472 0.423 −0.895 0.8954 360 7 1700 1400 0.454 0.429 −0.883 0.8831 968 8 1800 1400 0.477 0.451 −0.928 0.9281 130 9 1 900 1400 0.649 0.456 −1.105 1.1106 34 表 2 不同预测模型的参数取值
Table 2. Parameter values of different prediction models
预测模型 A b 最大主应变 1.2938 −0.05884 最大剪应变 1.0347 −0.06581 Mises等效应变 1.3559 −0.05953 最大主应力 552.8398 −0.01735 SWT 715.9432 −0.07639 表 3 不同寿命预测模型的预测误差
Table 3. Prediction errors of different life prediction models
预测模型 平均误差/% 最大主应变 58.50 最大剪应变 69.33 Mises 等效应变 59.75 最大主应力 68.54 SWT 34.07 -
[1] Chang L, Zhou B B, Ma T H, et al. The difference in low cycle fatigue behavior of CP-Ti under fully reversed strain and stress controlled modes along rolling direction[J]. Materials Science and Engineering A, 2019,742:211−223. doi: 10.1016/j.msea.2018.11.003 [2] Peng J, Zhou C Y, Dai Q, et al. Fatigue and ratcheting behaviors of CP-Ti at room temperature[J]. Materials Science and Engineering A, 2014,59:329−337. [3] Chang L, Wen J B, Zhou C Y, et al. Uniaxial ratcheting behavior and fatigue life models of commercial pure titanium[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018,41(9):2024−2039. [4] Chang L, Ma T H, Zhou B B, et al. Comprehensive investigation of fatigue behavior and a new strain-life model for CP-Ti under different loading conditions[J]. International Journal of Fatigue, 2019,129(C):105220. [5] Ma T H, Gao N, Chang L, et al. Low-cycle fatigue behavior and life prediction of CP-Ti under non-proportional and multiaxial loading[J]. Engineering Fracture Mechanics, 2021,254:107930. doi: 10.1016/j.engfracmech.2021.107930 [6] Ma T H, Zhou C Y, Gao N, et al. Low cycle fatigue behavior of CP-Ti under multiaxial load-controlled mode at different multiaxial stress ratios[J]. International Journal of Fatigue, 2022,160:106868. doi: 10.1016/j.ijfatigue.2022.106868 [7] Zhao J Y, Lu Z, Zhou C Y, et al. In‐plane biaxial ratcheting effect and low‐cycle fatigue behavior of CP‐Ti based on DIC method[J]. Fatigue & Fracture of Engineering Materials & Structures, 2022,45(5):1464−1479. [8] Chang L, Zhou C Y, Peng J, et al. Creep behavior of CP-Ti TA2 at low temperature and intermediate temperature[J]. Rare Metal Materials and Engineering, 2017,46(6):1463−1468. doi: 10.1016/S1875-5372(17)30147-9 [9] Peng J, Zhou C Y, Dai Q, et al. Dwell fatigue and cycle deformation of CP-Ti at ambient temperature[J]. Materials & Design, 2015,71:1−16. [10] Sakane M, Isobe N. Tension-torsion multiaxial creep-fatigue lives of the Nickel-based superalloy alloy 738LC[J]. International Journal of Fatigue, 2022,155:106575. doi: 10.1016/j.ijfatigue.2021.106575 [11] Yamamoto T, Itoh T, Sakane M, et al. Creep-fatigue life of Sn-8Zn-3Bi solder under multiaxial loading[J]. International Journal of Fatigue, 2012,43:235−241. doi: 10.1016/j.ijfatigue.2012.04.007 [12] Zhang S D, Sakane M. Multiaxial creep-fatigue life prediction for cruciform specimen[J]. International Journal of Fatigue, 2007,29(12):2191−2199. doi: 10.1016/j.ijfatigue.2006.12.012 [13] Xu L, Kojima T, Itoh T. Creep–fatigue life evaluation of type 304 stainless steel under non-proportional loading[J]. International Journal of Pressure Vessels and Piping, 2021,194:104515. doi: 10.1016/j.ijpvp.2021.104515 [14] Conceptualization L X U, Conceptualization R Z W, Conceptualization L H E. On multiaxial creep–fatigue considering the non-proportional loading effect: Constitutive modeling, deformation mechanism, and life prediction[J]. International Journal of Plasticity, 2022: 103337. [15] Li D H, Shang D G, Yin X, et al. A novel fatigue-oxidation-creep life prediction method under non-proportional loading[J]. Engineering Failure Analysis, 2022,131:105805. doi: 10.1016/j.engfailanal.2021.105805 [16] Bertini L. Life predictions by three creep-fatigue interaction models: influence of multiaxiality and time-variable loadings[J]. Materials at High Temperatures, 1991,9(1):23−29. doi: 10.1080/09603409.1991.11689636 [17] Asayama T, Aoto K, Wada Y. Effect of nonproportional loading on creep-fatigue properties of 304 stainless steel at low strain ranges near the elastic region[J]. Nuclear Engineering and Design, 1993,139(3):299−309. doi: 10.1016/0029-5493(93)90172-6 [18] ASTM E8/E8 M-2013a. Standard test method for tension testing of metallic materials[S]. [19] Kulawinski D, Ackermann S, Glage A, et al. Biaxial low cycle fatigue behavior and martensite formation of a metastable austenitic cast TRIP steel under proportional loading[J]. Steel Research International, 2011,82(9):1141−1148. doi: 10.1002/srin.201100111 [20] Sakane M. Effect of multiaxial stress and strain on low cycle fatigue, creep and creep-fatigue lifetimes for type 304 steel cruciform and cubic specimens[J]. Materialwissenschaft und Werkstoffechnik, 2018,49(3):301−315. doi: 10.1002/mawe.201700206 [21] Nagel K, Kulawinski D, Henkel S. Characterization of stress-strain behavior of a cast TRIP steel under different biaxial planar load ratios[J]. Engineering Fracture Mechanics, 2011,78(8):1684−1695. doi: 10.1016/j.engfracmech.2011.02.021 [22] Xiao Lin, Song Kai, Gu Haicheng. Biaxial low cycle fatigue lifetime evaluation of Zircaloy-4[J]. Acta. Metall. Sin., 1999,(4):397−402. (肖林, 宋凯, 顾海澄. Zr-4双轴低周疲劳寿命估算[J]. 金属学报, 1999,(4):397−402.Xiao Lin, Song Kai, Gu Haicheng. Biaxial low cycle fatigue lifetime evaluation of Zircaloy-4[J]. Acta. Metall. Sin. , 1999 (4): 397-402. [23] Poncelet M, Barbier G, Raka B, et al. Biaxial high cycle fatigue of a type 304L stainless steel: Cyclic strains and crack initiation detection by digital image correlation[J]. European Journal of Mechanics / A Solids, 2010,29(5):810−825. doi: 10.1016/j.euromechsol.2010.05.002 [24] Takamoto I, Sakane M, Masateru O. High temperature multiaxial low cycle fatigue of cruciform specimen[J]. Journal of Engineering Materials and Technology, 1994,116(1):90−98. doi: 10.1115/1.2904261 [25] Cláudio R, Reis L, Freitas M. Biaxial high-cycle fatigue life assessment of ductile aluminum cruciform specimens[J]. Theoretical and Applied Fracture Mechanics, 2014,73:82−90. doi: 10.1016/j.tafmec.2014.08.007 -
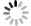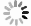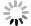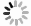




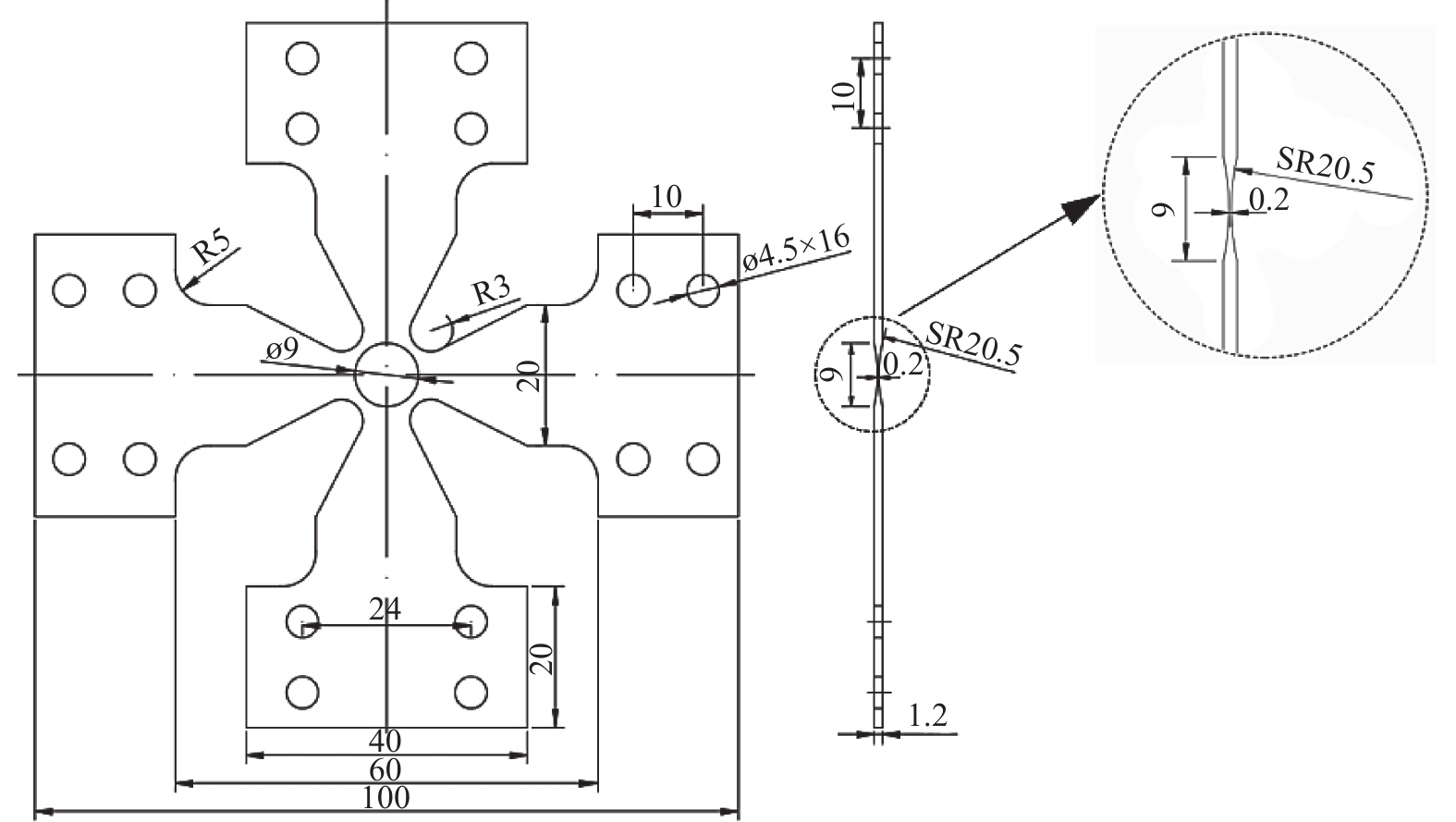
 下载:
下载: