Rheological behaviours and constitutive models of 9Cr18Mo stainless steel at high temperature and high strain rate
-
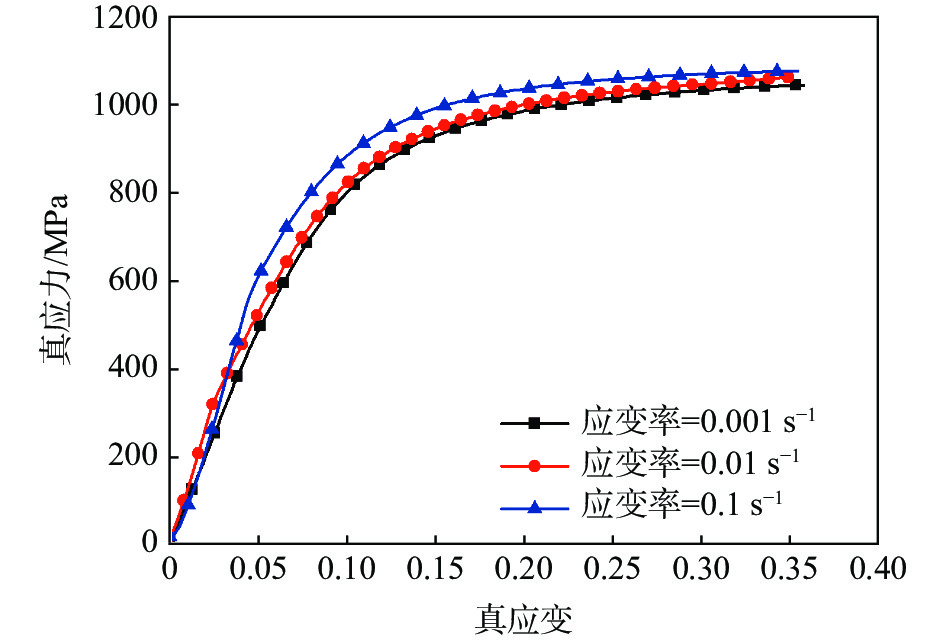
摘要: 在UTM5305万能试验机和剖分式 Hopkinson 压杆试验装置上,对9Cr18Mo不锈钢进行了压缩试验研究,获得准静态(应变率为0.001~0.1 s−1)及动态下(温度范围为25~650 ℃,应变率范围为800~4000 s−1)的应力—应变曲线关系。由获取的应力—应变曲线,探讨了其高温度、高应变率下的流变行为。依据所得到的试验数据,对其进行了J-C、P-L两种本构模型参数的识别,并对比分析了两种本构模型的相关系数(R)和平均相对误差(AARE)。结果表明,9Cr18Mo不锈钢具有应变率敏感性和显著的温度软化效应,即其流动应力随着应变率的增加而增加,随着温度的升高而显著下降。两种本构模型的相关系数(R)分别为0.9697、0.9896,平均相对误差(AARE)分别为2.77%、1.85%,即P-L本构模预测精度要高于J-C本构模型,更能精确地描述其高温、高应变率下的流变行为。
-
关键词:
- 9Cr18Mo不锈钢 /
- 流变行为 /
- 本构模型 /
- 相关性系数 /
- 平均相对误差
Abstract: The compression tests of 9Cr18Mo stainless steel were conducted by using the UTM5305 universal testing machine and the split Hopkinson pressure bar (SHPB) test device. In this way, the stress–strain curves pertaining to quasi-static (strain rate: 0.001-0.1 s−1) and dynamic (temperature: 25-650 ℃ and strain rate: 800-4000 s−1) states were attained. According to the stress-strain curves, the rheological behaviours of 9Cr18Mo stainless steel at high temperature and high strain rate were discussed. Based on the testing data, the parameters of two constitutive models (Johnson-Cook (J-C) and Power-Law (P-L)) of 9Cr18Mo stainless steel were identified, and the correlation coefficients (R) and average absolute relative errors (AAREs) of the two constitutive models were compared. The results showed that 9Cr18Mo stainless steel presents strain rate sensitivity and significant thermal softening. That is the flow stress of 9Cr18Mo stainless steel increases with strain rate while significantly decreases with increasing temperature. The R values are 0.9697 and 0.9896, while the AAREs of two constitutive models are 2.77% and 1.85%, respectively. Hence, the P-L constitutive model shows a higher prediction accuracy which can describe the rheological behaviours of 9Cr18Mo stainless steel at high temperature and high strain rate more precisely compared with the J-C constitutive model. -
图 12
$ \ln (\sigma ({\varepsilon _s},{\dot \varepsilon _s})/g({\varepsilon _s})) $ 和$ \ln (1 + {\dot \varepsilon _s}/{\dot \varepsilon _0}) $ 的关系Figure 12. Relationship between
$ \ln (\sigma ({\varepsilon _s},{\dot \varepsilon _s})/g({\varepsilon _s})) $ and$ \ln (1 + {\dot \varepsilon _s}/{\dot \varepsilon _0}) $ 表 1 试样化学成分
Table 1. Chemical composition of the sample
% C Si Cr Ni Mn P S Mo Fe 0.99 0.70 18.0 0.40 0.68 0.03 0.02 0.59 Bal. 表 2 不同试验条件下两种本构模型绝对误差的平均值
Table 2. Average absolute error of two constitutive models under different experimental conditions
T/℃ $ \dot \varepsilon $/s−1 $ \Delta {\sigma _{{\text{JC}}}} $/MPa $ \Delta {\sigma _{{\text{PL}}}} $/MPa T/℃ $ \dot \varepsilon $/s−1 $ \Delta {\sigma _{{\text{JC}}}} $/MPa $ \Delta {\sigma _{{\text{PL}}}} $/MPa 25 800 6.424471638 6.109457399 500 800 32.79624831 17.3101421 1500 38.98703638 15.33518007 1500 28.39327725 23.19058462 2000 37.04814443 9.391618684 2000 45.03536918 39.11484364 2500 29.46215782 5.722001128 2500 49.39455932 46.36667909 3000 22.34984852 5.923465121 3000 41.94325487 45.30685472 4000 5.982440216 3.902910575 4000 9.845891459 10.62832331 350 800 27.04190337 10.60611432 650 800 31.25790377 30.58632256 1500 20.1336439 18.2893326 1500 49.19664884 27.14529 2000 40.92181462 37.65429567 2000 51.54404536 26.74278264 2500 42.34938154 41.79854765 2500 33.93195871 11.88201571 3000 29.80158046 36.78908546 3000 26.76224827 9.985216708 4000 12.46319636 11.87826906 4000 20.68909126 15.5467803 -
[1] Liu Zhenbao, Liang Jianxiong, Su Jie, et al. Research and development status of high-strength stainless steel[J]. Acta Metallurgica Sinica, 2020,56(4):449−554. (刘振宝, 梁剑雄, 苏杰, 等. 高强度不锈钢的研究及发展现状[J]. 金属学报, 2020,56(4):449−554.Liu Zhenbao, Liang Jianxiong, Su Jie, et al. Research and development status of high-strength stainless steel[J]. Acta Metallurgica Sinica, 2020, 56(4): 449-554. [2] Young Ben, Lui Wingman. Behavior of cold-formed high strength stainless steel sections[J]. Journal of Structural Engineering, 2005,131(11):1738−1745. doi: 10.1061/(ASCE)0733-9445(2005)131:11(1738) [3] Ehab Ellobody, Young Ben. Structural performance of cold-formed high strength stainless steel columns[J]. Journal of Constructional Steel Research, 2005,61:1631−1649. doi: 10.1016/j.jcsr.2005.05.001 [4] Yang Zhiyong, Liu Zhenbao, Liang Jianxiong, et al. Development of maraging stainless steel[J]. Journal of Materials and Heat Treatment, 2008,(4):1−7. (杨志勇, 刘振宝, 梁剑雄, 等. 马氏体时效不锈钢的发展[J]. 材料热处理学报, 2008,(4):1−7.Yang Zhiyong, Liu Zhenbao, Liang Jianxiong, et al. Development of maraging stainless steel[J]. Journal of Materials and Heat Treatment, 2008, (4): 1-7. [5] Zerilli F J, Armstrong R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations[J]. J. Appl. Phys, 1987,61(5):1816−1825. doi: 10.1063/1.338024 [6] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[J]. Engineering Fracture Mechanics, 1983,21:541−548. [7] Samantaray D, Mandal S, Borah U, et al. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel[J]. Materials Science & Engineering A, 2009,526(1-2):1−6. [8] Kong Jinxing, Chen Hui, He Ning, et al. Dynamic mechanical properties test and constitutive model of pure iron material[J]. Journal of Aeronautics, 2014,35(7):2063−2071. (孔金星, 陈辉, 何宁, 等. 纯铁材料动态力学性能测试及本构模型[J]. 航空学报, 2014,35(7):2063−2071.Kong Jinxing, Chen Hui, He Ning, et al. Dynamic mechanical properties test and constitutive model of pure iron material [J]. Journal of Aeronautics, 2014, 35 (7): 2063-2071. [9] Tanimura S, Tsuda T, Abe A, et al. Comparison of rate-dependent constitutive models with experimental data[J]. International Journal of Impact Engineering, 2014,69(7):104−113. [10] 何著, 赵寿根, 杨嘉陵, 等, 0Cr17Ni4Cu4Nb不锈钢动态力学性能研究[J]. 材料科学与工程学报, 2007, 25(3): 418-421.He Zhu, Zhao Shougen, Yang Jialing, et al. Research on dynamic mechanical properties of 0Cr17Ni4Cu4Nb stainless steel[J]. Journal of Materials Science and Engineering, 2007, 25(3): 418-421. [11] Yan Hongzhi, Gong Lijun. Constitutive model and finite element simulation of 20CrMo material[J]. Journal of Central South University (Science and Technology), 2012,43(11):4268−4273. (严宏志, 龚黎军. 20CrMo材料本构模型及其有限元模拟[J]. 中南大学学报(自然科学版), 2012,43(11):4268−4273.Yan Hongzhi, Gong Lijun. Constitutive model and finite element simulation of 20 CrMo material[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4268-4273. [12] Forni D, Chiaia B, Cadoni E. Strain rate behaviour in tension of S355 steel: Base for progressive collapse analysis[J]. Engineering Structures, 2016,119(15):164−173. [13] Tuazon B J, Bae K O, Lee S H, et al. Integration of a new data acquisition/processing scheme in SHPB test and characterization of the dynamic material properties of high-strength steels using the optional form of Johnson-Cook model[J]. Procedia Economics & Finance, 2014,18(9):544−551. [14] Huang Yong, Liang Steven Y. Modelling of CBN tool crater wear in finish hard turning[J]. International Journal of Advanced Manufacturing Technology, 2004,24(9-10):632−639. doi: 10.1007/s00170-003-1744-5 [15] Samantaray D, Mandal S, K Bhaduri A, et al. An overview on constitutive modelling to predict elevated temperature flow behaviour of fast reactor structural materials[J]. Transactions of the Indian Institute of Metals, 2010,63(6):823−831. doi: 10.1007/s12666-010-0126-6 [16] 周惠久, 黄明志. 金属材料强度学[M]. 北京: 科学出版社, 1989.Zhou Huijiu, Huang Mingzhi. Strength of metallic materials[M]. Beijing: Science Press, 1989. [17] 王礼立. 冲击动力学进展[M]. 合肥: 中国科学技术大学出版社, 1992.Wang Lili. Progress in impact dynamics[M]. Hefei: University of Science and Technology of China Press, 1992. [18] Xu Z, Li Y. Dynamic behaviors of 0Cr18Ni10Ti stainless steel welded joints at elevated temperatures and high strain rates[J]. Mechanics of Materials, 2009,41(2):121−130. doi: 10.1016/j.mechmat.2008.10.005 [19] Yu Jianchao, Jiang Feng, Rong Yiming, et al. Numerical study the flow stress in the machining process[J]. International Journal of Advanced Manufacturing Technology, 2014,74(1-4):509−517. doi: 10.1007/s00170-014-5966-5 [20] 张兵, 岳磊, 陈韩锋, 等. 铸态GH4169合金热变形行为及三种本构模型对比[J]. 稀有金属材料与工程, 2021, 50(1): 212-222.Zhang Bing, Yue Lei, Chen Hanfeng, et al. Hot deformation behavior of as-cast GH4169 alloy and comparison of three constitutive models [J]. Rare Metal Materials and Engineering, 2021, 50(1): 212-222. [21] Sheikhali A H, Morakkabati M. Constitutive modeling for hot working behavior of SP-700 titanium alloy[J]. Journal of Materials Engineering and Performance, 2019,28(10):6525−6537. doi: 10.1007/s11665-019-04355-x -




 下载:
下载: