Research on damage failure of TA18 titanium alloy based on stress triaxiality
-
摘要: 对TA18钛合金材料设计不同缺口尺寸的拉伸试样,进行不同应力状态下的室温拉伸试验及断口形貌观察,通过试验和数值计算结合的方法研究TA18钛合金的韧性断裂特性,分析了应力状态对微观断裂机制的影响规律。利用Bridgman正向计算法修正颈缩失稳后的应力数据,建立了TA18钛合金的Johnson-Cook(J-C)本构模型,计算了拉伸试样的平均应力三轴度和断裂应变,回归确定了TA18钛合金损伤失效模型。结果表明:不同应力状态下的TA18钛合金断裂应变各不相同,断裂应变随着应力三轴度的增大而减小,断口韧窝尺寸与应力三轴度呈正相关关系,所建立的损伤失效模型能够描述该材料的断裂特性。Abstract: Tensile specimens made of TA18 titanium alloy with different notch sizes were designed to carry out tensile tests under different stress states at room temperature, and fracture morphology observation had been done. The ductile fracture characteristics of TA18 titanium alloy were studied through the combination of experiment and numerical calculation. The influence law of stress state on microscopic fracture mechanism had been analyzed. The Bridgman forward calculation method was used to correct the stress data after necking instability. The Johnson-Cook (JC) constitutive model of TA18 titanium alloy was established, and the average stress triaxiality and fracture strain of the tensile specimen were calculated and determined by the regression method. The damage failure model of TA18 titanium alloy is presented. The results show that the fracture strain of TA18 titanium alloy under different stress states is different. The fracture strain decreases with the increase of stress triaxiality, and the fracture dimple size is positively correlated with the stress triaxiality. The established damage failure model can explain the fracture characteristics of the material.
-
Key words:
- TA18 titanium alloy /
- ductile fracture /
- stress triaxiality /
- damage failure /
- numerical simulation
-
0. 引言
TA18(Ti-3Al-2.5V)是一种近α型钛合金,具有良好的力学性能、耐腐蚀性和焊接性,广泛应用于航空航天、石油化工等先进制造领域[1-2]。在TA18钛合金构件制备和服役过程中,复杂的外部载荷极易使构件表面产生裂纹而最终断裂失效[3-4]。因此,研究TA18钛合金材料的损伤行为和断裂机制,实现损伤失效的有效预测,对于减少制造缺陷和预防服役失效具有重要意义。
研究表明复杂的应力状态和累积应变量是引起韧性材料断裂的主要因素[5-7]。为了研究金属材料的断裂机理与失效函数关系,常引入应力三轴度这一状态参数,结合损伤力学、微观断裂机制建立相关的韧性准则。叶宏德等[8]研究了应力三轴度对10CrNiCu钢韧性断裂的影响,对临界损伤参数Wdc和J-C失效参数进行了标定,得出应力三轴度与韧窝的尺寸呈正比的结论。余万千等[9]分别采用拉伸、压缩等试验并与数值计算结合,对30CrMnSiNi2A钢的韧性断裂特性进行了研究。陈继恩[10]以14MnNbq材料为研究对象,通过力学试验对不同应力三轴度范围内断裂应变随应力三轴度的变化规律进行了研究。李棠[11]利用宏观力学试验和微观断口形貌观察研究了2A12铝合金的韧性断裂特点,分析了应力三轴度和失效应变的相关性。
为了研究TA18钛合金的室温损伤失效机制,笔者制备了不同缺口尺寸的试样,进行室温拉伸断裂试验,结合有限元模拟和微观表征等手段,分析了应力三轴度对材料拉伸性能和韧性断裂机制的影响,探究不同应力状态下微观孔洞的演化规律。基于试验数据应用J-C断裂理论,对TA18钛合金的J-C失效模型参数进行了标定与校核。
1. 拉伸试验与方法
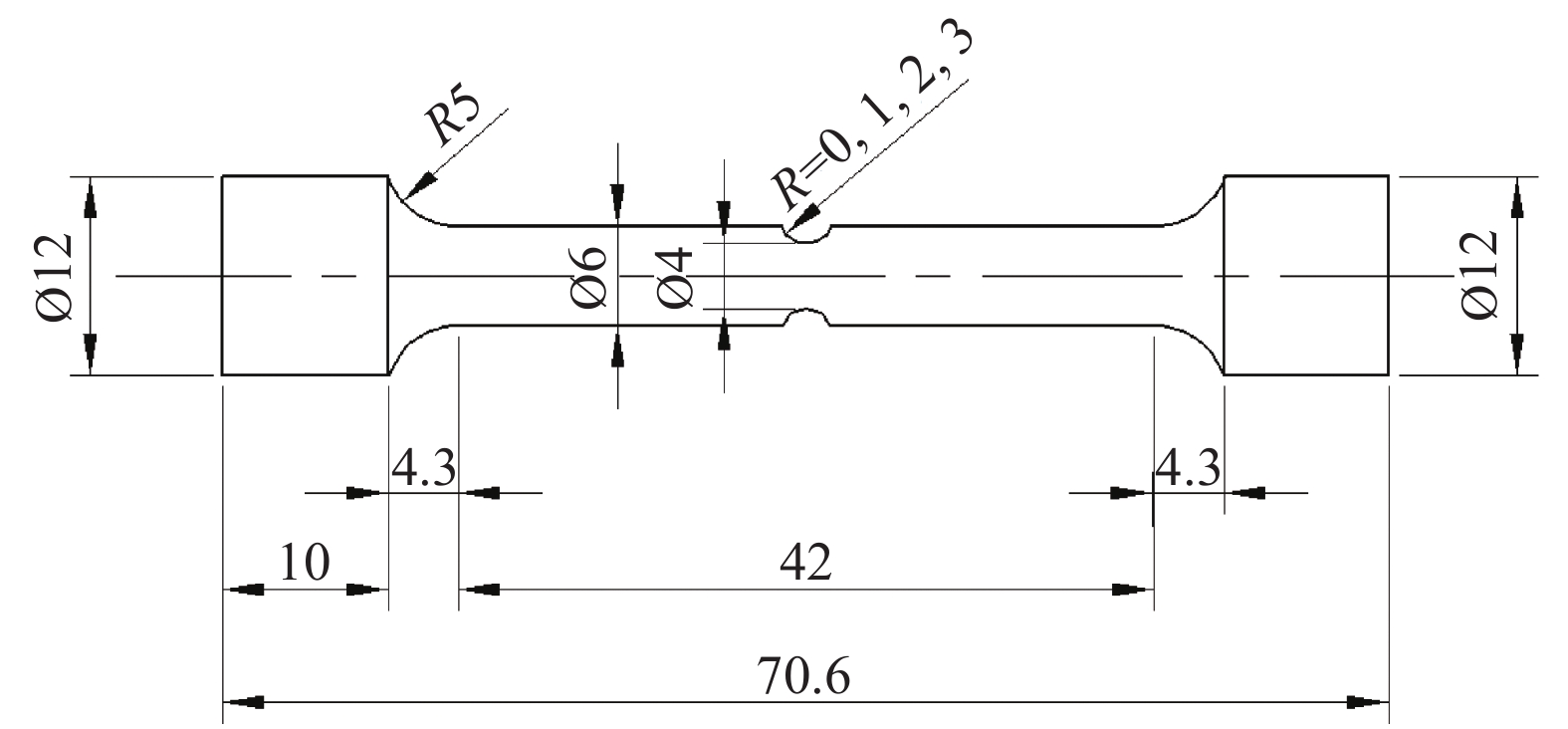
试样取自TA18钛合金冷轧前的管坯,沿管坯轴向AD(轧制方向)进行取样和加工。依据GB/T 228.1—2010标准制备了不同尺寸缺口的试样,研究材料在不同应力三轴度下的破坏特性与断裂机制。选取缺口半径R分别为0、1、2、3 mm的试样(见图1)进行室温单轴拉伸试验,试样代号依次用SRB、NR1、NR2和NR3表示。TA18钛合金成分如表1所示。
表 1 TA18钛合金的化学成分Table 1. Chemical composition of TA18 titanium alloy% Al V Fe C N O H Ti 2.75 2.5 0.25 0.08 0.05 0.12 0.015 余量 在MTS-SANS CMT5305系列电子万能试验机上进行静态拉伸试验,如图2所示,拉伸速率为5 mm/min,每组试验重复3次,取均值。试样断口特征采用JEOLJSM-7900F型扫描电镜进行观察和分析,研究不同应力三轴度下的韧性断裂机理。
2. 试验结果与分析
2.1 试样拉伸试验
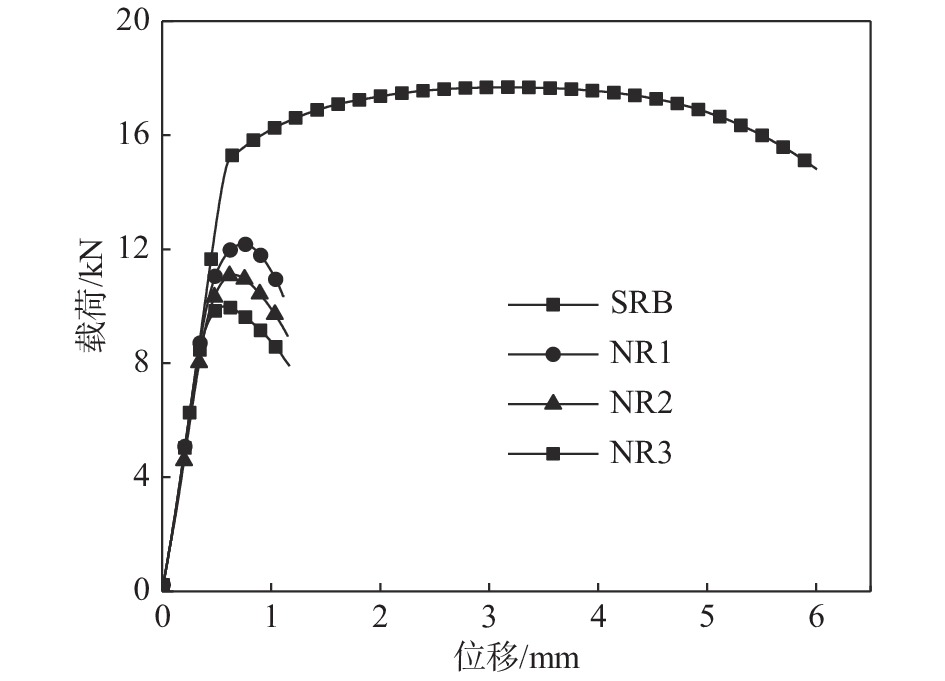
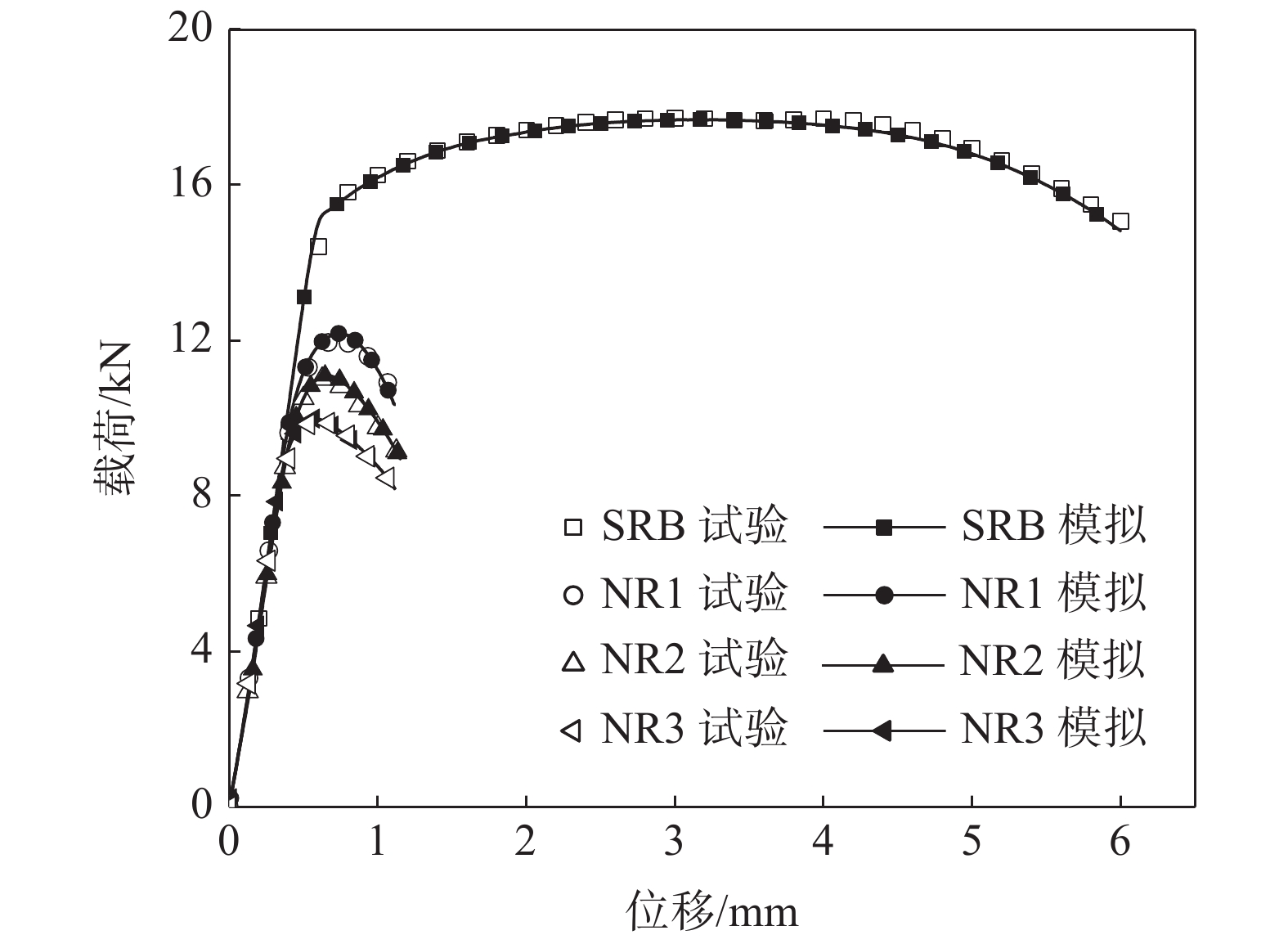
图3、4为5 mm/min拉伸速率下各试样的位移载荷曲线及断裂形貌。由图3可知,无缺口试样发生明显颈缩后断裂,塑性屈服强度Rp0.2为550 MPa,抗拉强度Rm为625 MPa,断后延伸率可达15.8%。而带缺口试样的颈缩程度不明显,断裂位置均位于缺口最小截面处。不同缺口尺寸的试样加载曲线弹性段基本重合,而断裂伸长量随缺口半径的增大而增大,名义屈服载荷和极限载荷均随缺口半径的增大而减小,表明缺口半径越大塑性越好。
2.2 断口宏微观形貌观察
采用扫描电镜(SEM)观察各试件断口形貌(图4),可知不同试样的拉伸断口均为杯锥状。断口主要由中心处粗糙的纤维区与边缘的剪切唇区组成,放射区不明显。起裂首先发生在中心区域的纤维区,当裂纹扩展到试样外表面时产生剪切唇,剪切唇与拉伸载荷方向成光亮45º角。这些断口均呈现出典型的韧性断裂。
图5为断口中心区域的微观形貌。试件的断口处分布了许多大小不同的微孔、韧窝,大韧窝旁分布有大量的孔洞和小韧窝。金属材料断裂通常归因于外力作用导致的内部孔洞形核、长大与聚合[12]。在拉伸过程中,材料内部的夹杂物或第二相粒子诱导空穴形核、长大和聚合,持续加载达到材料的屈服极限时,材料开始发生塑性变形。当局部应力超过第二相粒子和界面的强度时,夹杂物或第二相粒子间的基体部分形成内缩颈,形成微孔洞与宏观裂纹汇合导致撕裂或剪切断裂,内部孔洞交融在一起形成裂纹源,最终扩展形成典型的韧窝[13-14]。
金属材料在复杂应力状态下的断裂损伤一般采用应力三轴度进行表征,缺口半径越小应力三轴度越大。由图5(a)可知,对于无缺口试样R=0 mm,断口整体较为平整,均匀分布了大量微孔洞,这些微孔洞小而浅,孔洞数量远远大于韧窝数量。图5(b)~(d)分别对应缺口尺寸R为1、2、3 mm时的断口形貌。NR1试样应力三轴度最大,韧窝数量最多,且大小不同、形状各异,表现为高韧性断裂。NR2试样韧窝数量较前者减少,并且韧窝深度变浅,韧性降低。NR3试样断口形貌上只有少量小而浅的韧窝,孔洞数量较多。因此,随着应力三轴度的增大,韧窝大小和深度增大,微孔洞数量不断减少。这是由于缺口试样从加载开始一直处于三向应力状态,促进孔洞不断发生聚合进而生成大小不同的韧窝;并且应力三轴度越大,孔洞径向扩张越快,越容易发生聚合,从而韧窝数量也越多,孔洞数量随之减少,材料的塑性变形能力越强。
3. 材料本构方程建立
3.1 有限元建模
使用有限元软件Abaqus-Explicit进行拉伸试验的模拟,所建立的各缺口试样有限元模型如图6所示。为了提高计算效率、简化模型,只对标距内的试样部分进行模拟,并对标距段中部的网格进行局部细化。按照实际试验工况对边界条件与载荷部分进行设置。
3.2 本构方程建立
考虑到缺口试样最小横截面半径和缺口轮廓曲率半径的变化规律,采用Bridgman正向计算法[15]对不同尺寸缺口试样颈缩后的复杂应力状态下(单轴转变为三轴)的真实应力数据进行修正。由图3中位移载荷曲线关系得到工程应力-应变曲线,再根据式(1)和式(2)求解真应力-应变曲线。
$$ \sigma_{t}=\sigma_{e}\left(1+\varepsilon_{t}\right) $$ (1) $$ {\varepsilon _t} = \ln (1 + {\varepsilon _e}) $$ (2) 式中σe和εe分别为工程应力和工程应变;σt和εt分别为真实应力和真实应变。
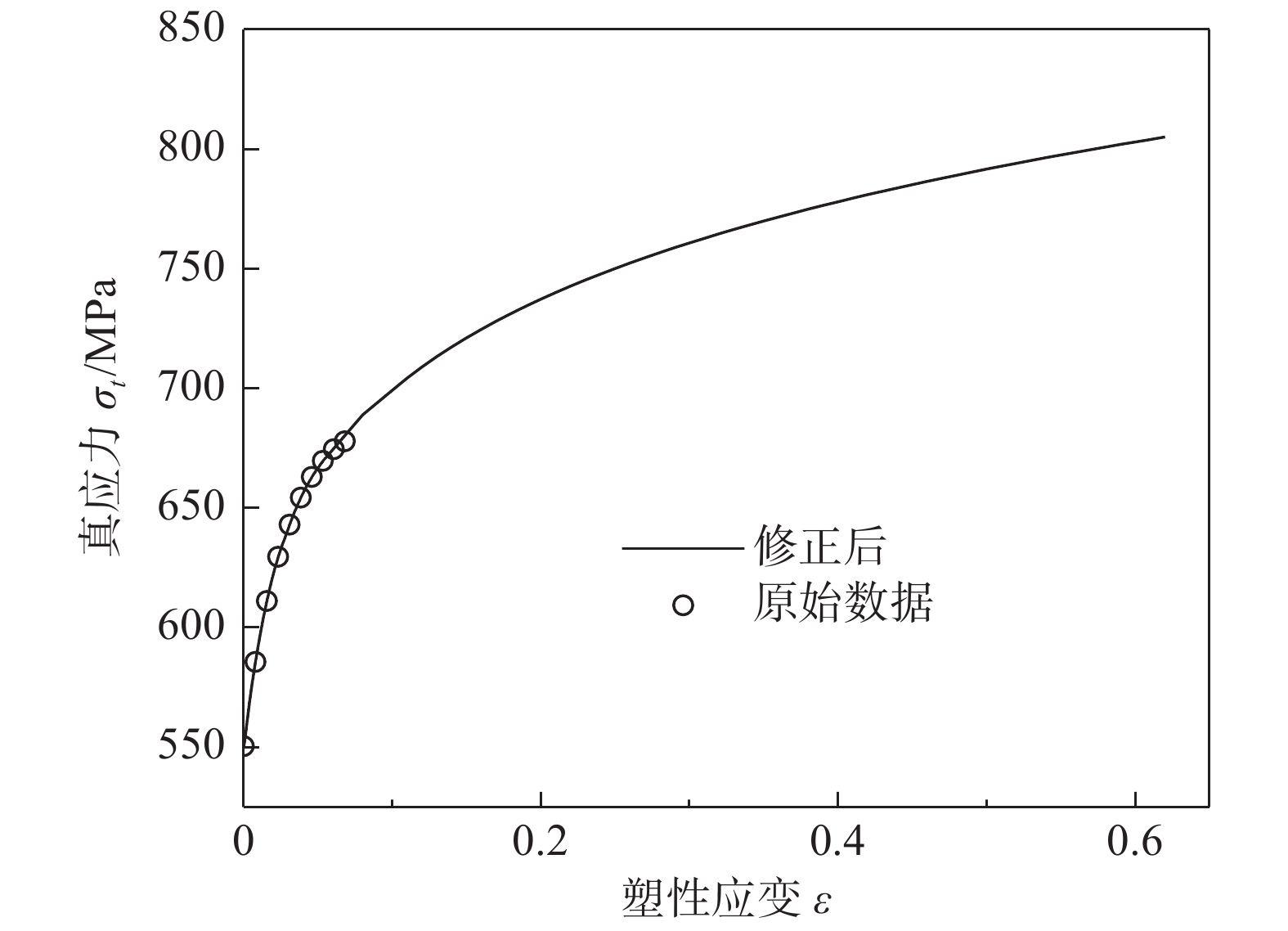
为了确定大应变下TA18钛合金的硬化曲线,通过有限元迭代法对无缺口SRB试样颈缩后的应力应变曲线进行反求,直到所得位移-载荷曲线的计算值与试验值基本重合,从而得到大应变条件下的真实应力应变曲线修正值,如图7所示。
采用简化的J-C方程建立TA18钛合金的本构模型,通过对修正后无缺口SRB试样的真应力应变数据进行拟合,得到TA18钛合金在室温拉伸条件下的本构方程,如式(3):
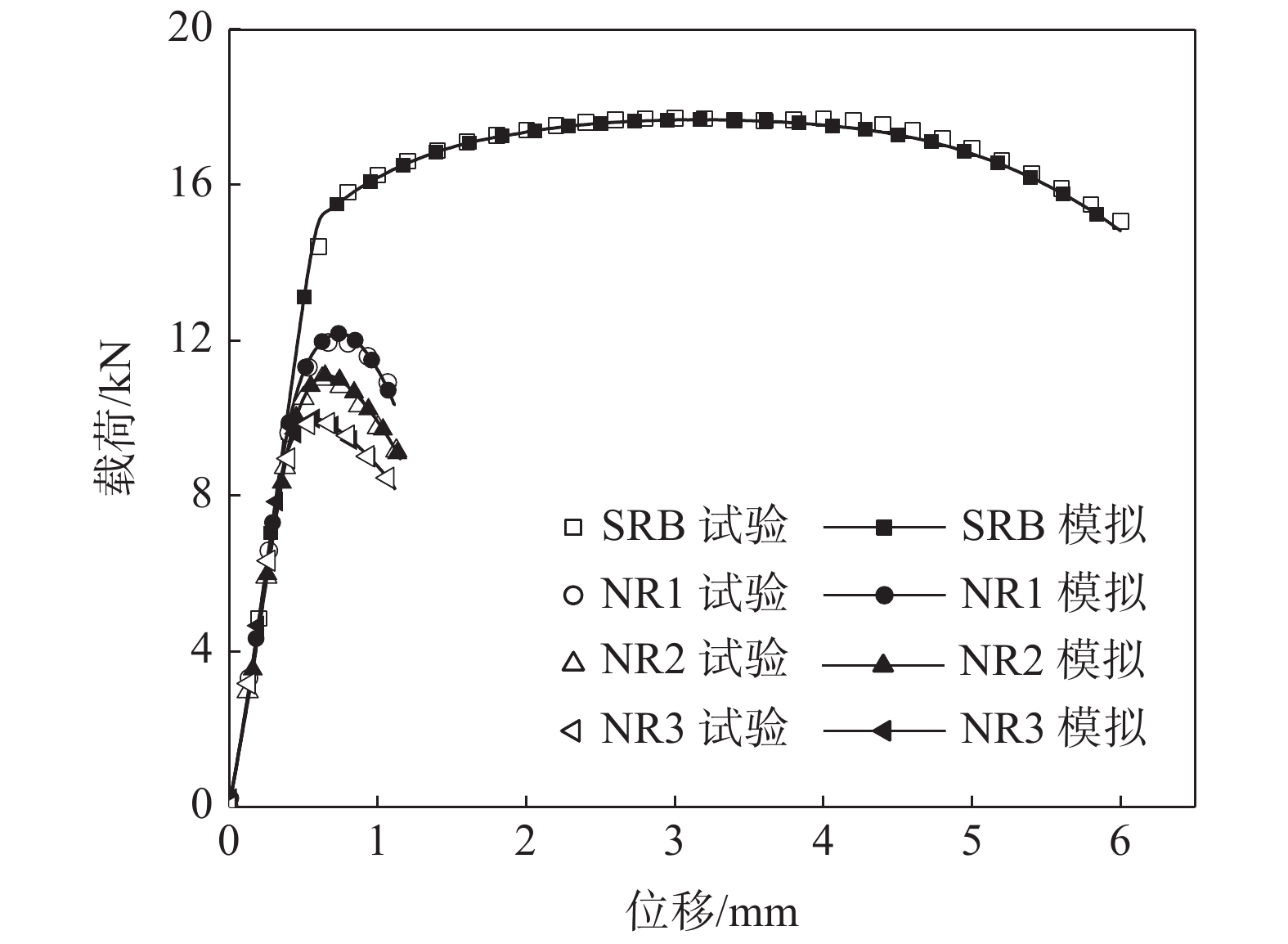
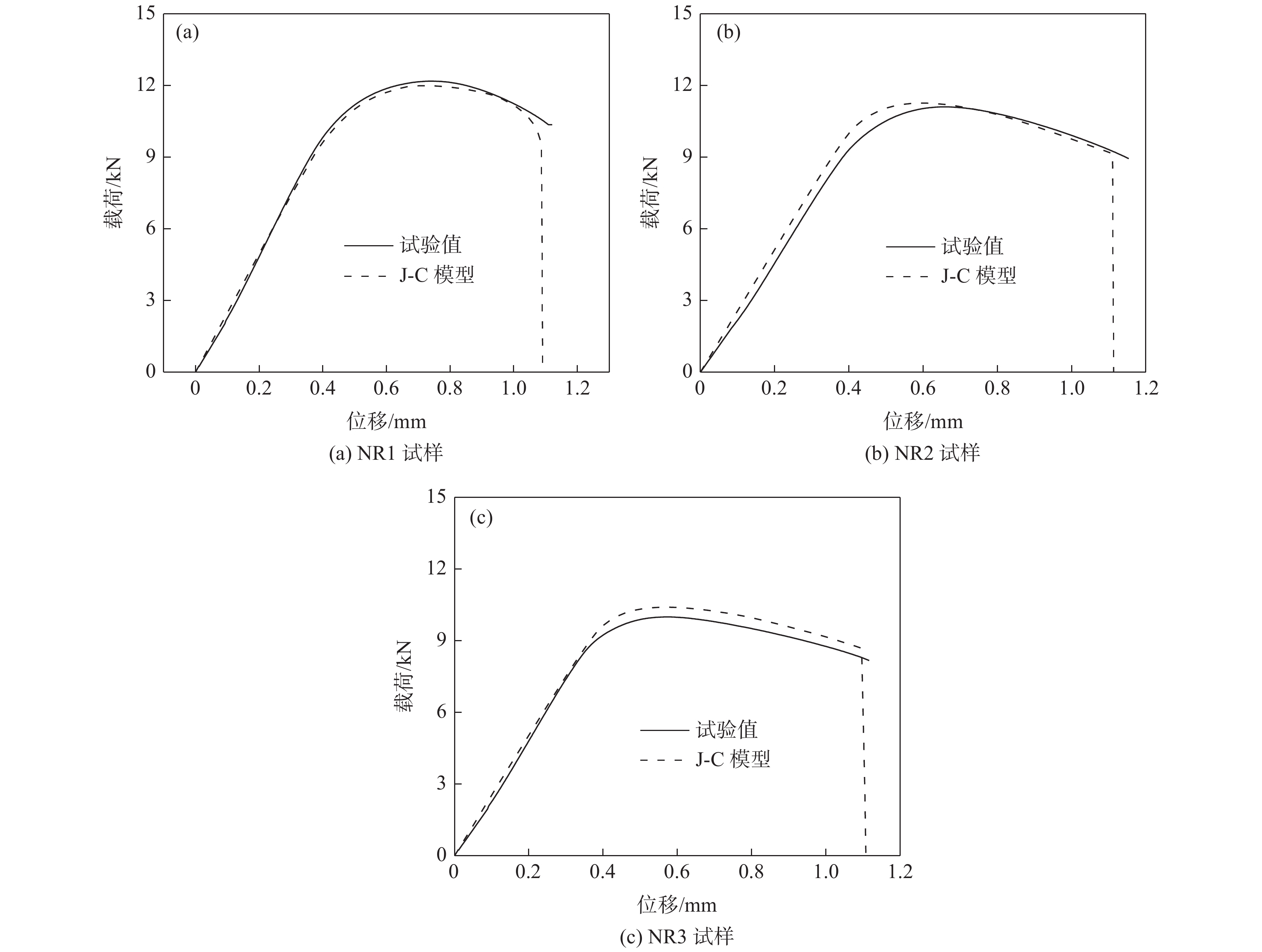
$$ {\sigma }_{e}=550.407+294.296{\varepsilon }_{ep}^{0.309} $$ (3) 基于上述J-C本构模型对不同缺口尺寸的试样进行拉伸过程模拟,得到不同缺口试样位移-载荷的模拟值与试验结果比较曲线,如图8所示,两者吻合良好(R2≈0.97),验证了所建本构模型的可靠性。
4. 基于应力三轴度的损伤失效模型
4.1 应力三轴度演变规律
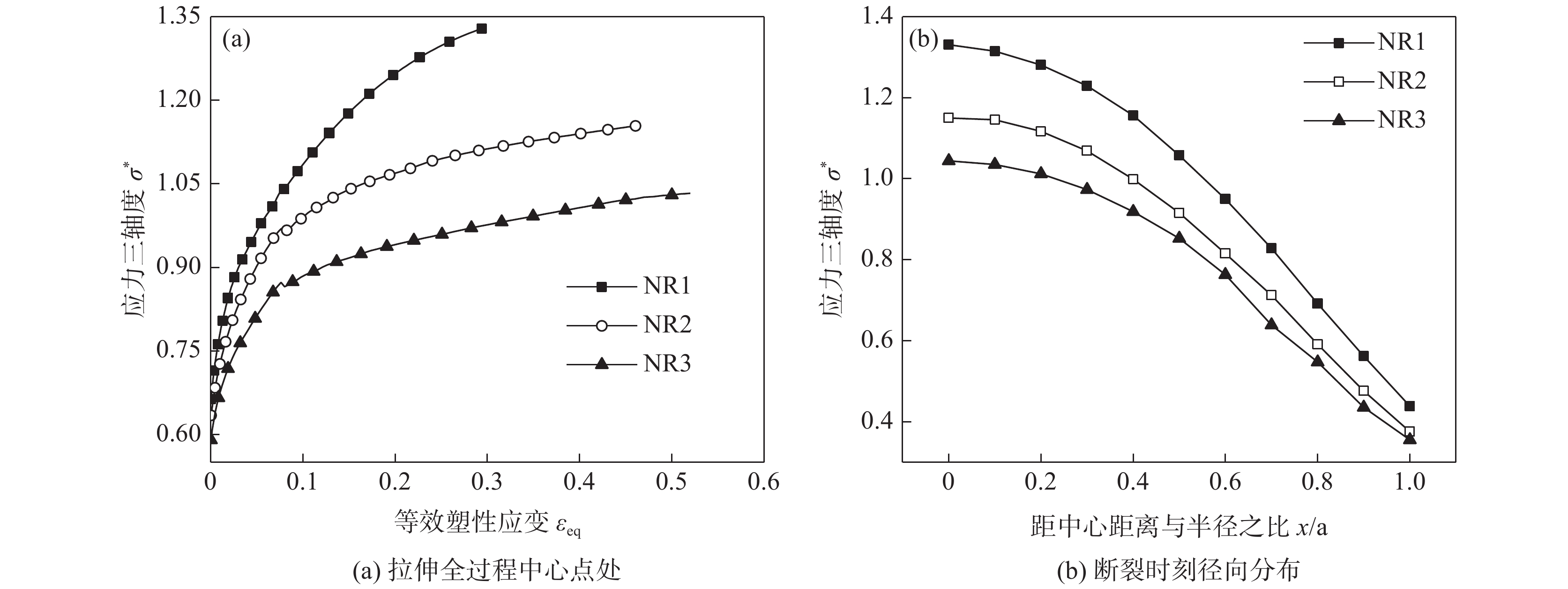
基于上述所建立的TA18本构方程进行拉伸过程的有限元模拟,可得到不同缺口尺寸试样在不同时刻、不同截面路径上的应力三轴度分布规律(图9)。由图9(a)可知在拉伸过程中,缺口中心处应力三轴度随等效塑性应变的增加均呈上升趋势,归因于试样拉伸过程中颈缩面不断减小;由图9(b)可知缺口试样截面径向的应力三轴度的分布趋势基本相同,均从中心沿径向逐渐减小,缺口半径越小应力三轴度越大。
由图9(a)可知,带缺口试样截面的应力三轴度分布存在明显的应变累积效应,采用平均应力三轴度作为研究韧性断裂的衡量指标,一点处平均应力三轴度的定义表达式为[16]:
$$ \sigma _{{\text{av}}}^{\text{*}} = \frac{1}{{\overline {{\varepsilon _f}} }}\int_0^{\overline {{\varepsilon _f}} } {\sigma (\overline \varepsilon } )d\overline \varepsilon $$ (4) 式中,
$ {\sigma }_{{\rm{av}}}^{*} $ 为平均应力三轴度;$\overline{\varepsilon }$ 为等效塑性应变;$\overline{{\varepsilon }_{f}}$ 为断裂应变。根据材料体积不变的假设,带缺口试样的断裂应变可通过拉伸前后最小截面处的半径求得,其计算公式为:
$$ {\varepsilon }_{f}=2\mathrm{ln}\left(\frac{{a}_{0}}{{a}_{f}}\right) $$ (5) 式中,
$ {a}_{0} $ 为初始缺口半径;$ {a}_{f} $ 为试件断裂时的最小横截面半径。利用式(4)与式(5)可得各试样的平均应力三轴度与断裂参数(表2),平均应力三轴度随缺口半径的增大而减小,由R=1 mm时的1.136减小至R=3 mm时的0.941,断裂应变由R=1 mm时的0.452增加至R=3 mm时的0.625。
表 2 不同试样的断裂参数Table 2. Fracture parameters of different samples缺口半径/
mm初始直径/
mm断裂应变
εf断裂直径/
mm应力三轴度 初始值 最终值 平均值 1 4.20 0.452 3.35 0.670 1.330 1.136 2 4.15 0.520 3.2 0.628 1.152 1.047 3 4.10 0.625 3.0 0.596 1.030 0.941 4.2 损伤失效模型的建立
由图2和图4可知TA18钛合金的拉伸断裂失效形式为韧性断裂,即外载作用下的损伤累积到一定程度时导致金属完全失稳断裂。根据损伤力学理论,当损伤变量D大于1时,材料即发生失效,J-C损伤失效模型是基于累积损伤准则的典型损伤失效模型,将累计损伤变量D定义为[17]:
$$ D = \sum {\frac{{\Delta {\varepsilon _{eq}}}}{{{\varepsilon _f}}}} $$ (6) 式中,D为损伤变量;
$\Delta {\varepsilon _{eq}} $ 为一个积分循环中等效塑性应变增量;${\varepsilon _{f}}$ 为当前循环中的有效断裂应变。考虑室温拉伸断裂应变值与应力三轴度的关系,J-C损伤失效模型可简化为:$$ {\varepsilon _f} = ({D_1} + {D_2}\exp ({D_3}{\sigma ^*})) $$ (7) 采用式(7)对表2中断裂应变与应力三轴度数据进行拟合,可得TA18钛合金在室温拉伸条件下J-C损伤失效模型为:
$$ {\varepsilon }_{f}=\left(0.145+4.334\mathrm{e}\mathrm{x}\mathrm{p}\left(-2.663{\sigma }^{*}\right)\right) $$ (8) 将基于J-C损伤失效模型的模拟结果与试验结果进行了对比(图10),结果表明位移-载荷曲线的模拟值与试验值吻合度较高。缺口试样拉伸的有限元模拟与试验断裂结果如图11所示,试样均在缺口位置最小截面处断裂,其扩展路径与断裂位置基本一致。验证了室温拉伸条件下该损伤失效模型的准确性。
5. 结论
1) 以TA18钛合金为研究对象,开展了不同应力状态下的拉伸断裂试验,建立了室温拉伸条件下TA18钛合金材料的J-C本构方程:
$ {\sigma }_{e}=550.407+ $ $ 294.296{\varepsilon }_{ep}^{0.309} $ 。2) 通过不同缺口尺寸试样拉伸试验的断口形貌观察,发现试样断口处均分布大小不同、形状各异的韧窝与空洞,呈现高应力三轴度下典型的韧性断裂特征;基于应力三轴度进行了断裂失效机制分析,表明随着应力三轴度的增加,塑性变形加剧,断裂应变逐渐减小,韧窝尺寸变大,微孔数量逐渐减少。
3) 建立了TA18钛合金损伤失效模型,并通过数值模拟手段进行模型验证,得到损伤失效模型为:
$ {\varepsilon }_{f}=\left(0.145+4.334\mathrm{e}\mathrm{x}\mathrm{p}\left(-2.663{\sigma }^{*}\right)\right) $ 。 -
表 1 TA18钛合金的化学成分
Table 1. Chemical composition of TA18 titanium alloy
% Al V Fe C N O H Ti 2.75 2.5 0.25 0.08 0.05 0.12 0.015 余量 表 2 不同试样的断裂参数
Table 2. Fracture parameters of different samples
缺口半径/
mm初始直径/
mm断裂应变
εf断裂直径/
mm应力三轴度 初始值 最终值 平均值 1 4.20 0.452 3.35 0.670 1.330 1.136 2 4.15 0.520 3.2 0.628 1.152 1.047 3 4.10 0.625 3.0 0.596 1.030 0.941 -
[1] Yang Jianchao, Xi Jinhui, Yang Yashe, et al. Development and application of TA18 titanium alloy tube for aerospace use[J]. Titanium Industry Progress, 2014,31(4):6−10. (杨建朝, 席锦会, 杨亚社, 等. 航空航天用TA18钛合金管材的研发及应用[J]. 钛工业进展, 2014,31(4):6−10. [2] Jiang Zhiqiang, Yang He, Zhan Mei, et al. Development and prospects of titanium alloy pipes and their applications in the aviation field[J]. Journal of Plasticity Engineering, 2009,16(4):44−50,842. (江志强, 杨合, 詹梅, 等. 钛合金管材研制及其在航空领域应用的现状与前景[J]. 塑性工程学报, 2009,16(4):44−50,842. doi: 10.3969/j.issn.1007-2012.2009.04.010 [3] Li Heng, Wei Dong, Yang Heng, et al. Research trends and existing problems of high-performance pipe two-roll Pilger cold rolling forming[J]. Aeronautical Manufacturing Technology, 2018,61(21):16−24. (李恒, 魏栋, 杨恒, 等. 高性能管材二辊皮尔格冷轧成形研究动态及存在问题[J]. 航空制造技术, 2018,61(21):16−24. [4] Yuan Hongjun, Li Yonglin, Zhao Hongzhang, et al. Cause analysis of cold rolling cracking of TA18 titanium alloy tube[J]. Hot Working Technology, 2014,43(23):163−165. (袁红军, 李永林, 赵洪章, 等. TA18钛合金管冷轧开裂原因分析[J]. 热加工工艺, 2014,43(23):163−165. [5] Wang Tiejun. Further investigation of a new continuum damage mechanics criterion for ductile fracture: Experimental verification and applications[J]. Engineering Fracture Mechanics, 1994,48(2):217−230. [6] Park Sung Ju, Cerik Burak Can, Choung Joonmo. Comparative study on ductile fracture prediction of high-tensile strength marine structural steels[J]. Ships and Offshore Structures, 2021,15(S1):208−219. [7] Bao Yingbin, Tomasz Wierzbicki. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004,46(1):81−98. doi: 10.1016/j.ijmecsci.2004.02.006 [8] Ye Hongde, Dang Hengyao, Li Hui, et al. Research on notched tensile properties and critical damage parameters of marine 10CrNiCu steel[J]. China Shipbuilding, 2019,60(2):50−58. (叶宏德, 党恒耀, 李慧, 等. 船用10CrNiCu钢缺口拉伸性能及临界损伤参数研究[J]. 中国造船, 2019,60(2):50−58. doi: 10.3969/j.issn.1000-4882.2019.02.005 [9] Yu Wanqian, Yu Rui, Cui Shitang. Research on ductile fracture of 30CrMnSiNi2A steel considering the influence of stress triaxiality[J]. Explosion and Shock, 2021,41(3):47−54. (余万千, 郁锐, 崔世堂. 考虑应力三轴度影响的30CrMnSiNi2A钢韧性断裂研究[J]. 爆炸与冲击, 2021,41(3):47−54. [10] 陈继恩. 基于应力三轴度的材料失效研究[D]. 武汉: 华中科技大学, 2012.Chen Ji, en. Research on material failure based on stress triaxiality[D]. Wuhan: Huazhong University of Science and Technology, 2012. [11] Li Tang, Wang Qingyuan, Yue Zhufeng. Experimental study on ductile fracture mechanism of aluminum alloy 2A12[J]. Experimental Mechanics, 2006,(6):763−768. (李棠, 王清远, 岳珠峰. 铝合金2A12韧性断裂机制的实验研究[J]. 实验力学, 2006,(6):763−768. doi: 10.3969/j.issn.1001-4888.2006.06.013 [12] Rice J R, Tracey D M. On the ductile enlargement of voids in triaxial stress fields[J]. Journal of the Mechanics and Physics of Solids, 1969,17:201−217. doi: 10.1016/0022-5096(69)90033-7 [13] Zhong Peidao. Fracture failure analysis[J]. Physical Testing and Chemical Testing (Physics Section), 2005,(7):375−378. (钟培道. 断裂失效分析[J]. 理化检验(物理分册), 2005,(7):375−378. [14] Liu Lixi, Zheng Qingli, Zhu Jian, et al. The effect of stress triaxiality and Rhodes parameter on the ductile fracture of aluminum alloys (English)[J]. Rare Metal Materials and Engineering, 2019,48(2):433−439. (刘立熙, 郑清丽, 朱健, 等. 应力三轴度和罗德参数对铝合金韧性断裂的影响[J]. 稀有金属材料与工程, 2019,48(2):433−439. [15] Bridgman P W. Studies in large plastic flow and fracture with special emphasis on the effects of hydrostatic pressure [M]. New York: Mc Graw Hill, 1952. [16] Goto D M, Koss D A, Jablokov V. The influence of tensile stress states on the failure of HY-100 steel [J]. Metallurgical and Materials Transactions A, 1999,30A:2835−2842. [17] Johnson Gordon R, Cook William H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985,21(1):31−48. 期刊类型引用(3)
1. 张彪,刘家招,杨鑫三,孙宇萱. 基于XFEM的汽车铝合金断裂行为表征. 材料导报. 2024(19): 223-227 .  百度学术
百度学术2. 马春辉,张殿平,贡泽飞,付秋涛,刘兴峰,李迪. 先进高强双相钢板破裂失效B-W预测模型. 塑性工程学报. 2023(02): 214-222 .  百度学术
百度学术3. 张伟,刘华赛,桑贺,李春光,陈洪生,宋起峰. 残余奥氏体对双相钢断裂失效性能的影响. 塑性工程学报. 2023(11): 185-193 .  百度学术
百度学术其他类型引用(2)
-





 下载:
下载:








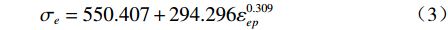

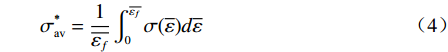
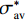

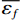





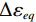
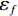
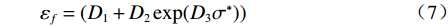
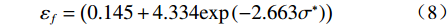



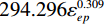
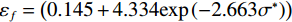

 下载:
下载:









 百度学术
百度学术