Tensile mechanical properties and constitutive model of commercial pure titanium TA2 welded joints at medium-low temperature
-
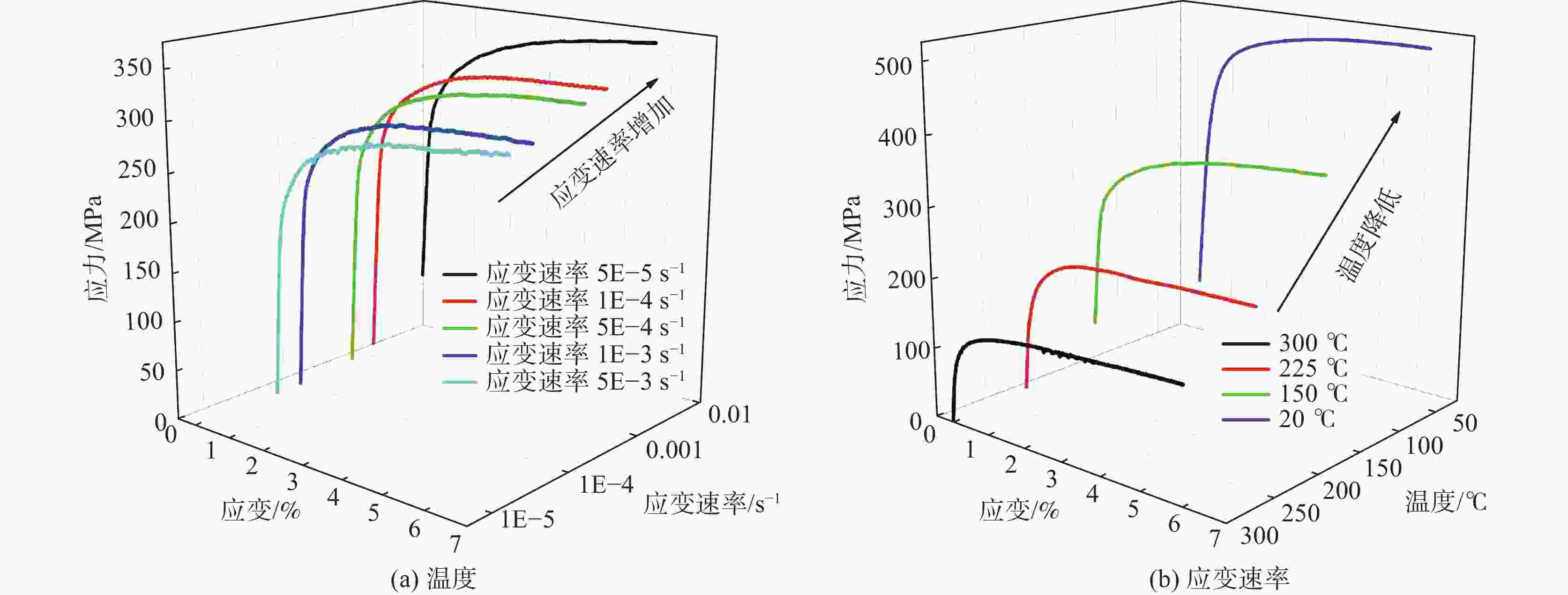
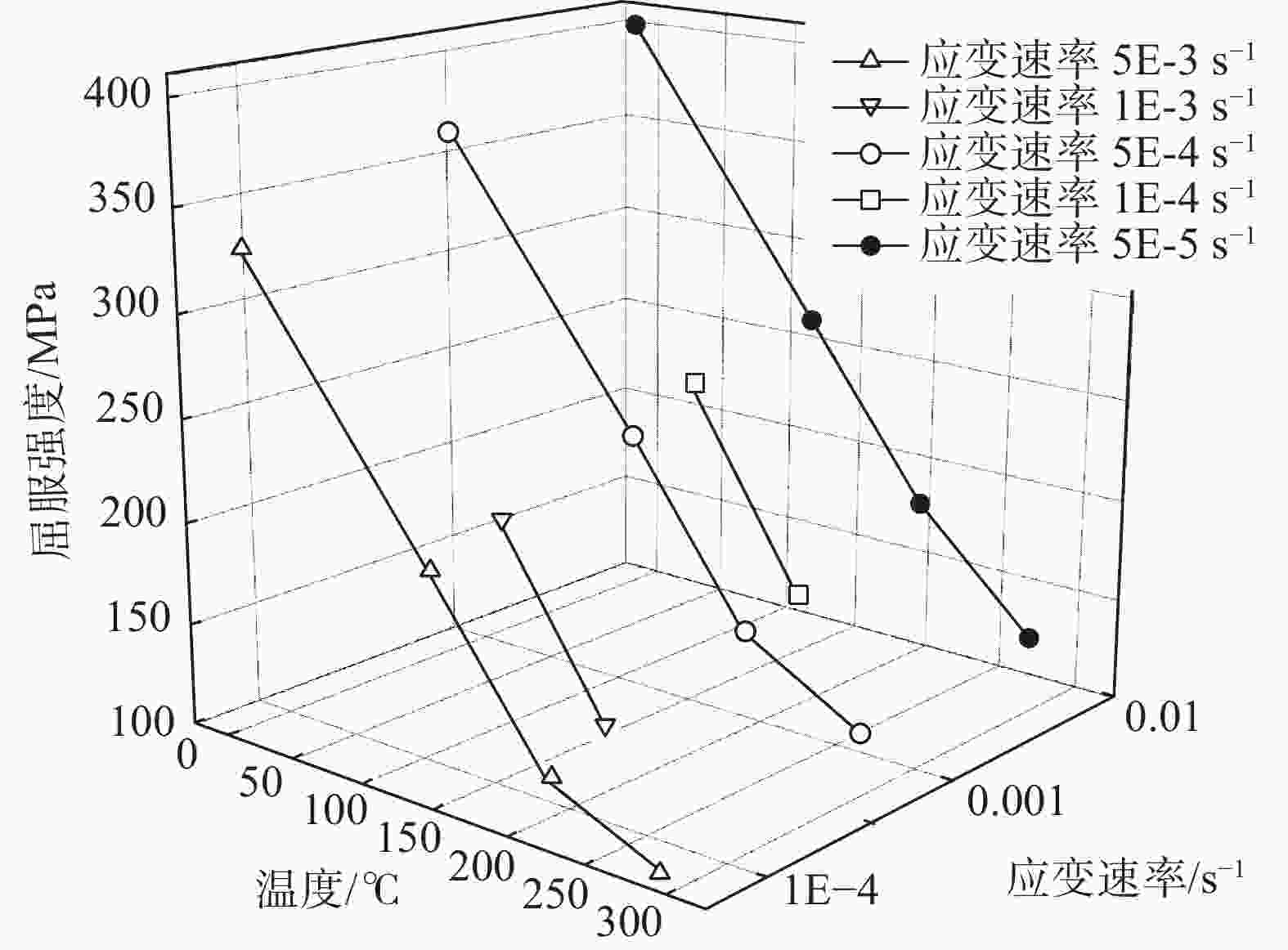
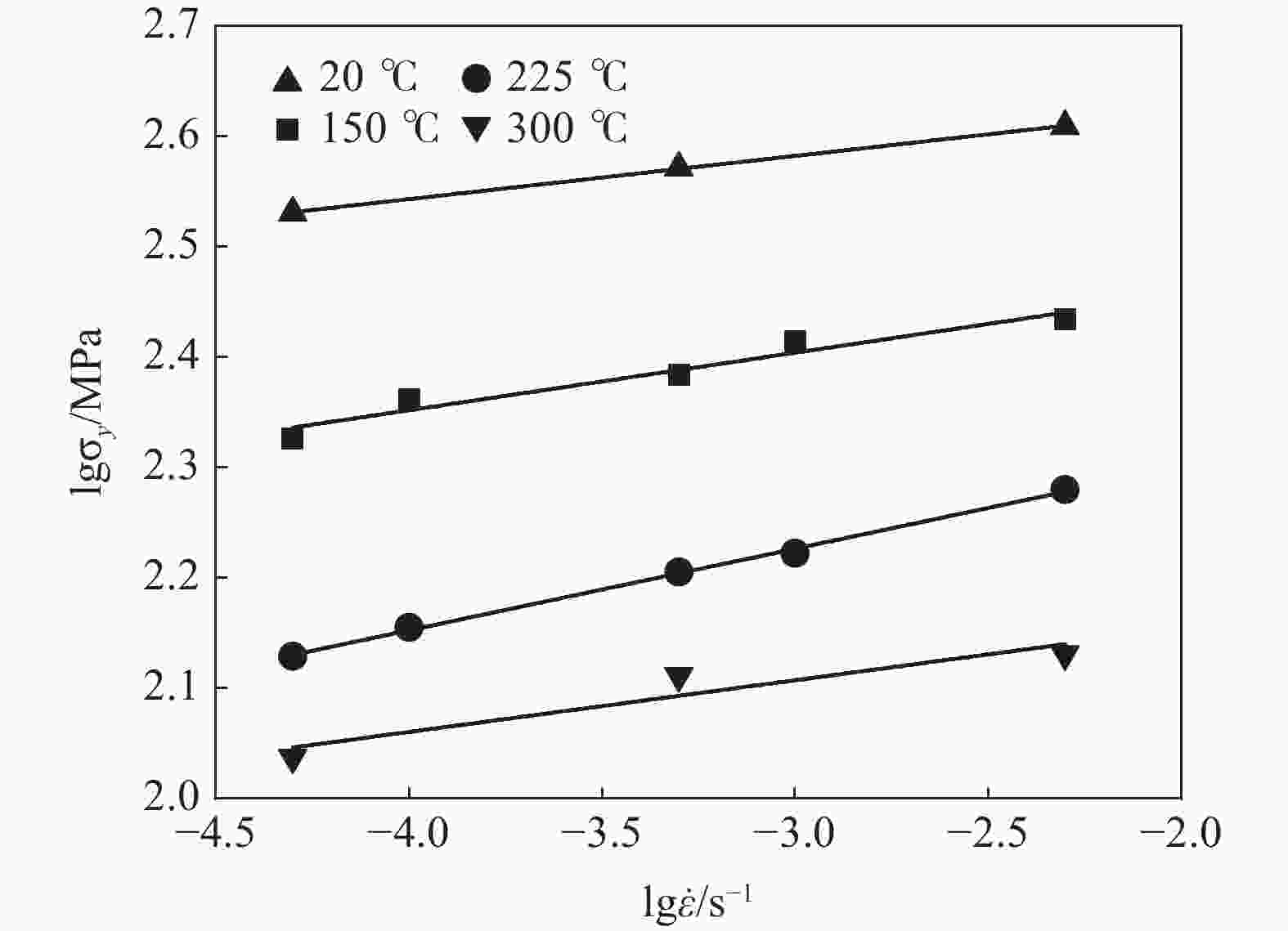
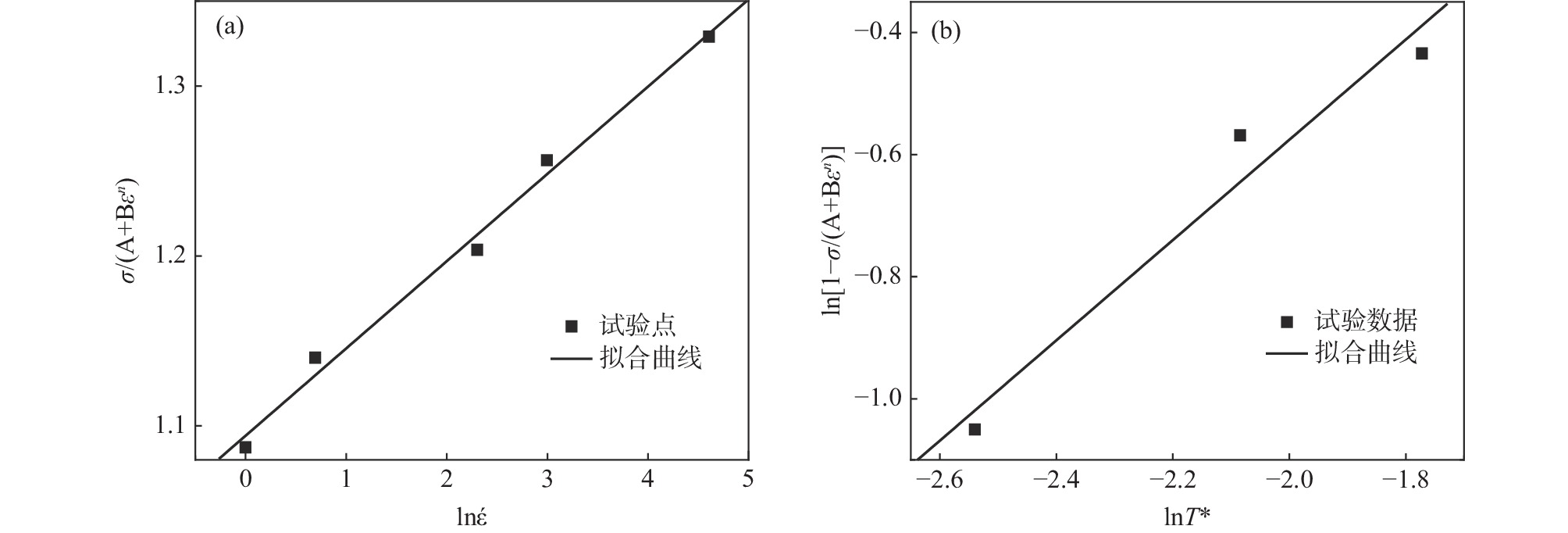
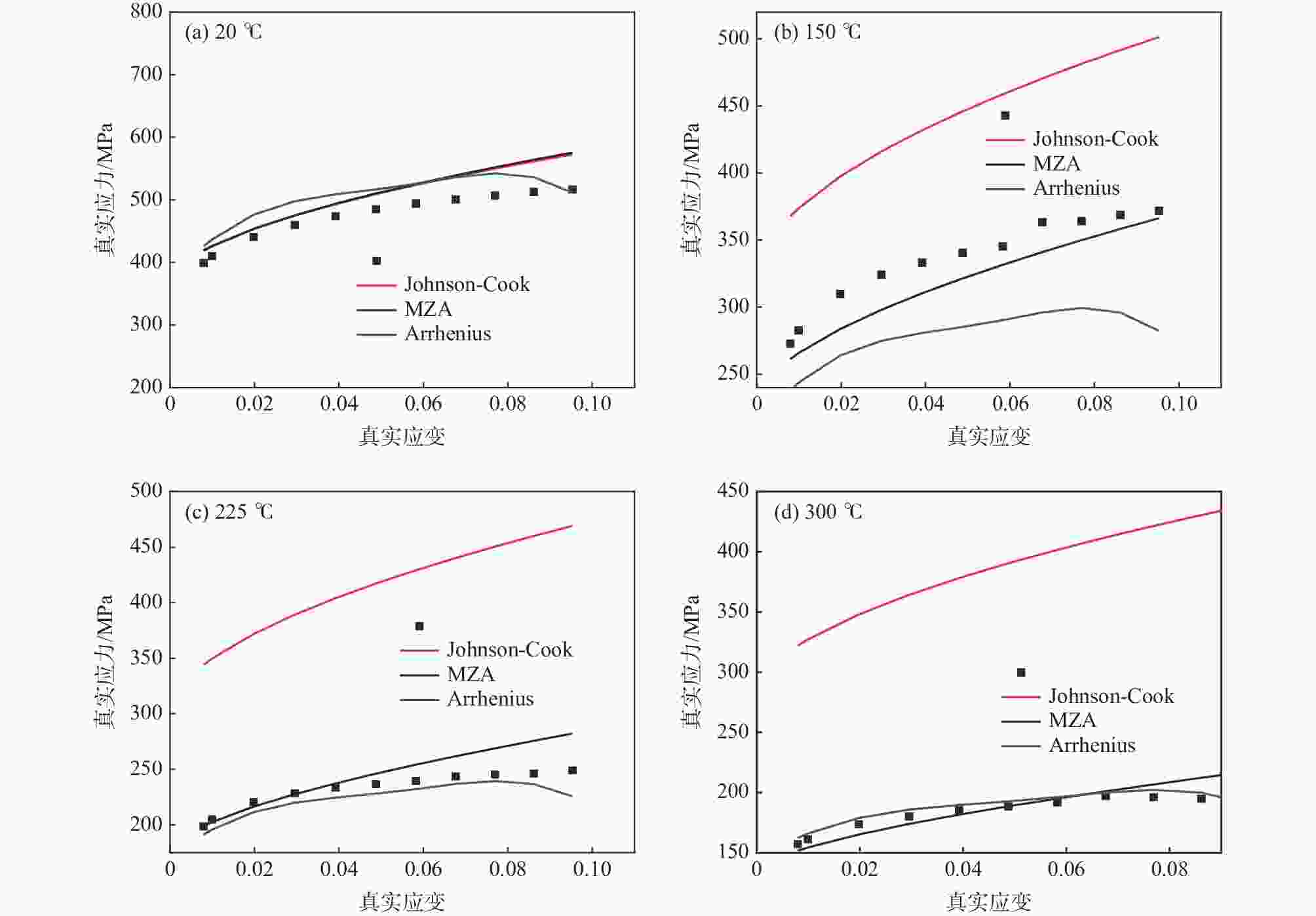
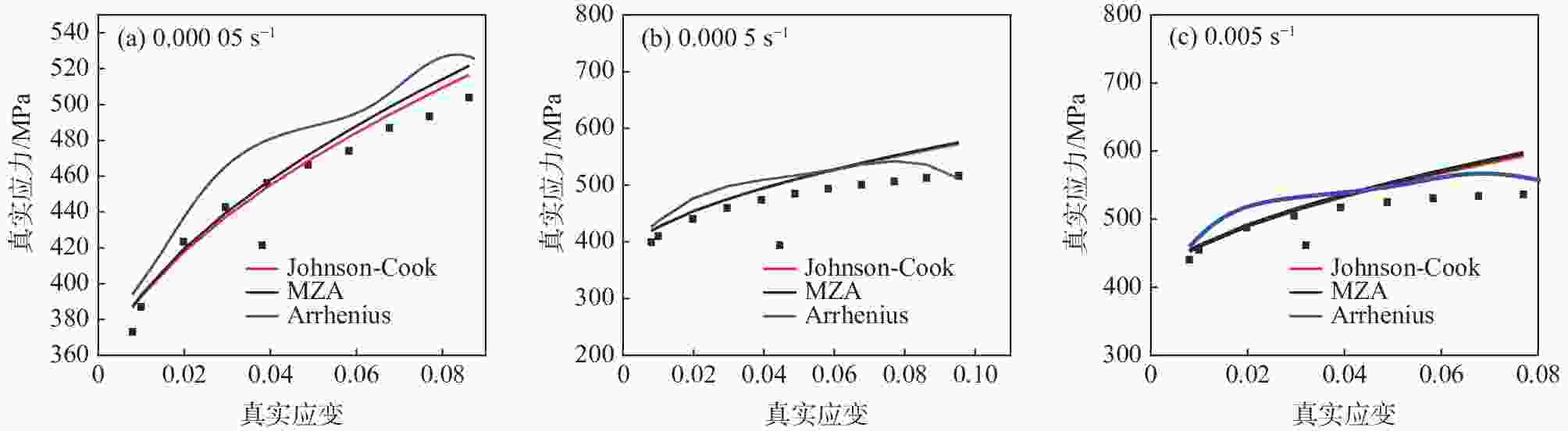
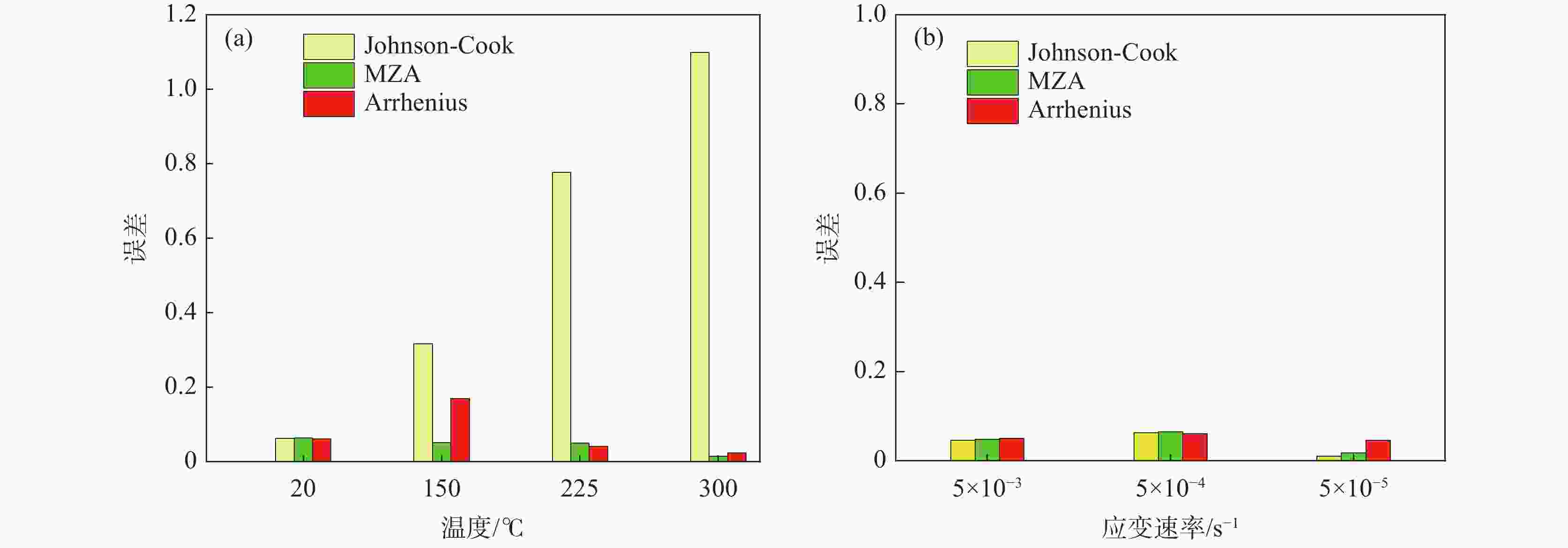
摘要: 以TA2工业纯钛焊接接头为研究对象,开展了不同温度和应变速率下的拉伸试验,分析了温度及应变速率对于材料强度及流变应力的影响。结果表明:TA2焊接接头的屈服强度与温度呈线性关系,与应变速率呈指数关系,并建立了屈服强度与温度和应变速率的经验公式。基于Arrhenius、Johnson-Cook (JC)及Modified Zerilli-Armstrong (MZA)本构方程,对工业纯钛焊接接头的中低温拉伸流变应力进行预测。将三种模型的预测值与试验值进行定量对比,发现JC模型预测精度最低,MZA模型预测精度最高。研究结果为钛材在承压设备中的应用提供数据支撑,有利于更好地设计、加工、制造和使用钛制承压设备。Abstract: In this paper, tensile tests of commercial pure titanium TA2 welded joints at different temperatures and strain rates were carried out to analyze the effects of temperature and strain rate on the flow stress and strength of the material. The yield strength of TA2 welded joints present a linear relationship with temperature and an exponential relationship with strain rate. The empirical formula between yield stress and temperature and strain rate was established. Based on the constitutive equations of Arrhenius, Johnson-Cook (JC) and Modified Zerili-Armstrong (MZA), the tensile flow stress of commercial pure titanium welded joints at medium-low temperature was predicted. The prediction accuracy of different constitutive models was quantitatively compared with experimental results. It was found that JC model has the lowest prediction accuracy and MZA model has the highest prediction accuracy. Current study provides data support for the application of titanium materials in pressure equipment, and it is useful for the design, manufacturing, fabrication and use of titanium pressure equipment.
-
表 1 拉伸试验方案
Table 1. Tensile test scheme
温度/℃ 应变速率/$ {\mathrm{s}}^{-1} $ 20 0.00005 0.0005 0.005 150 0.00005 0.0001 0.0005 0.001 0.005 225 0.00005 0.0001 0.0005 0.001 0.005 300 0.00005 0.0005 0.005 表 2 工业纯钛焊接接头的JC本构方程材料参数
Table 2. The JC constitutive parameters of TA2 welded joint
A B n C m 339 691.82988 0.55474 0.03776 0.8211 表 3 工业纯钛焊接接头的MZA本构方程材料参数
Table 3. The MZA constitutive parameters of TA2 welded joint
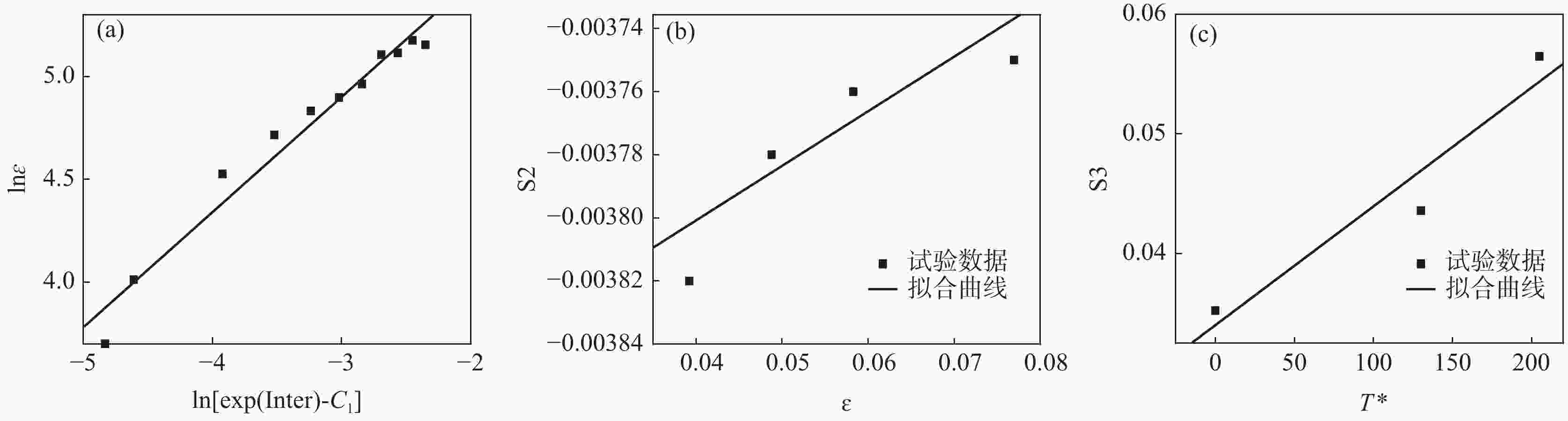
n $ {C_1} $ $ {C_2} $ $ {C_3} $ $ {C_4} $ $ {C_5} $ $ {C_6} $ 0.55963 339 720 0.00387 −0.00173 0.03401 0.0000993431 表 4 工业纯钛的 Arrhenius 本构方程材料参数
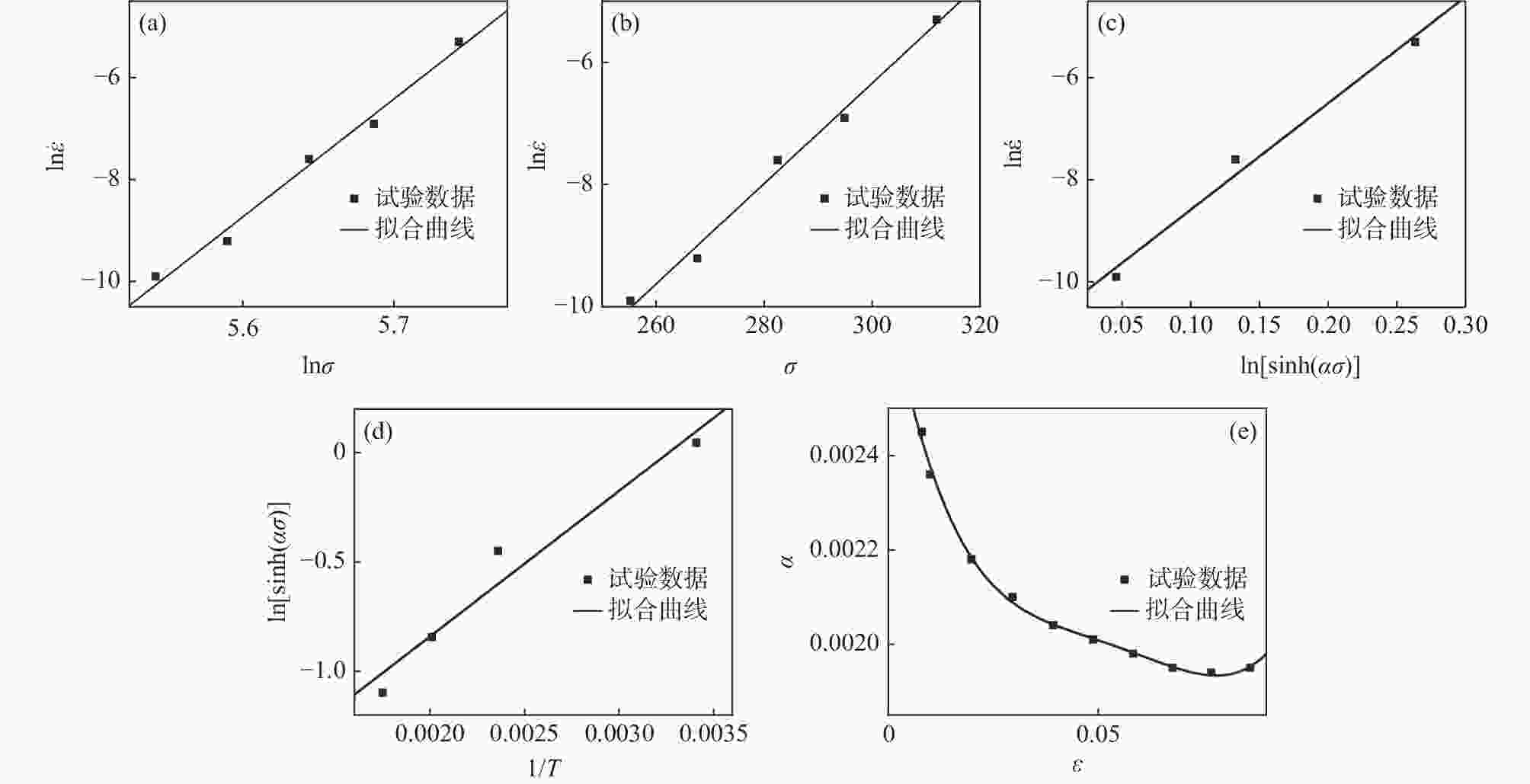
Table 4. The Arrhenius constitutive parameters of CP-Ti
$ \mathrm{I}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r} $ $ {b}_{1} $ $ {b}_{2} $ $ {b}_{3} $ $ {b}_{4} $ α 0.00274 −0.0475 1.26433 −15.78211 72.83189 n 40.51897 3597.53995 193783.7292 $ -3.7\times {10}^{6} $ $ -2.3\times {10}^{7} $ Q 224.76851 20043.62102 $ 1.09\times {10}^{6} $ $ -2.1\times {10}^{7} $ $ 1.3\times {10}^{8} $ $ \mathrm{ln}A $ 76.287 −7492.11985 406983.1909 $ -7.8\times {10}^{6} $ $ 4.94\times {10}^{7} $ 表 5 本构模型相关系数
$ {\mathit{R}}{{'}} $ 的比较Table 5. Comparison of correlation coefficient R' for different constitutive models
本构模型 参数数量 $ R' $ JC 5 0.817 MZA 7 0.887 Arrhenius 20 0.859 -
[1] Wang Hao. Application prospect of titanium[J]. China Metal Bulletin, 2011,(37):16−18. (王镐. 钛应用前景广阔[J]. 中国金属通报, 2011,(37):16−18. [2] Chang Le, Zhou Changyu, Peng Jian, et al. Fields–Backofen and a modified Johnson-Cook model for CP-Ti at ambient and intermediate temperature[J]. Rare Metal Materials and Engineering, 2017,46(7):1803−1809. doi: 10.1016/S1875-5372(17)30170-4 [3] Peng Jian, Zhou Changyu, Dai Qiao, et al. An improved constitutive description of tensile behavior for CP-Ti at ambient and intermediate temperatures[J]. Materials and Design, 2013,50:968−976. doi: 10.1016/j.matdes.2013.04.003 [4] Peng Jian, Zhou Changyu, Dai Qiao, et al. The temperature and stress dependent primary creep of CP-Ti at low and intermediate temperature[J]. Materials Science and Engineering A, 2014,611:123−135. doi: 10.1016/j.msea.2014.05.094 [5] Chang Le, Ma Tianhao, Zhou Binbin, et al. Comprehensive investigation of fatigue behavior and a new strain-life model for CP-Ti under different loading conditions[J]. International Journal of Fatigue, 2019,129:105220. doi: 10.1016/j.ijfatigue.2019.105220 [6] Chang Le, Zhou Binbin, Ma Tianhao, et al. The difference in low cycle fatigue behavior of CP-Ti under fully reversed strain and stress-controlled modes along rolling direction[J]. Materials Science & Engineering A, 2019,742:211−223. [7] Chang Le, Wen Jianbin, Zhou Changyu, et al. Uniaxial ratcheting behavior and fatigue life models of commercial pure titanium[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018,41(9):1−16. [8] Li Jian, Zhang Peng, Lu Lei, et al. Effect of pre-strain on fatigue crack growth behavior for commercial pure titanium at ambient temperature[J]. International Journal of Fatigue, 2018,117:27−38. doi: 10.1016/j.ijfatigue.2018.07.036 [9] Sun Pengyan, Zhu Zhikang, Lu Lei, et al. Experimental characterisation of mechanical behaviour for a TA2 welded joint using digital image correlation[J]. Optics and Lasers in Engineering, 2019,115:161−171. doi: 10.1016/j.optlaseng.2018.11.022 [10] Lu Lei, Li Jian, Su Chuanyi, et al. Research on fatigue crack growth behavior of commercial pure titanium base metal and weldment at different temperatures[J]. Theoretical and Applied Fracture Mechanics, 2019,100:215−224. doi: 10.1016/j.tafmec.2019.01.017 [11] Su Chuanyi, Zhou Changyu, Lu Lei, et al. Effect of temperature and dwell time on fatigue crack growth behavior of CP-Ti[J]. Metals, 2018,8(12):1031. doi: 10.3390/met8121031 [12] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]// Proceedings of the 7th International Symposium on Ballistics. Den Haag: The Netherlands, 1983: 541–543. [13] Shi H, McLaren A J, Sellars C M, et al. Constitutive equations for high temperature flow stress of aluminium alloys[J]. Mater Sci Technol, 13 (3): 210-216. [14] Samantaray D, Mandal S, Borah U, et al. Thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel[J]. Mater. Sci. Eng. A, 2009,(526):1−6. -




 下载:
下载: