Investigation on fatigue crack growth behavior of mixed mode Ⅰ-Ⅱ crack in 4130X steel
-
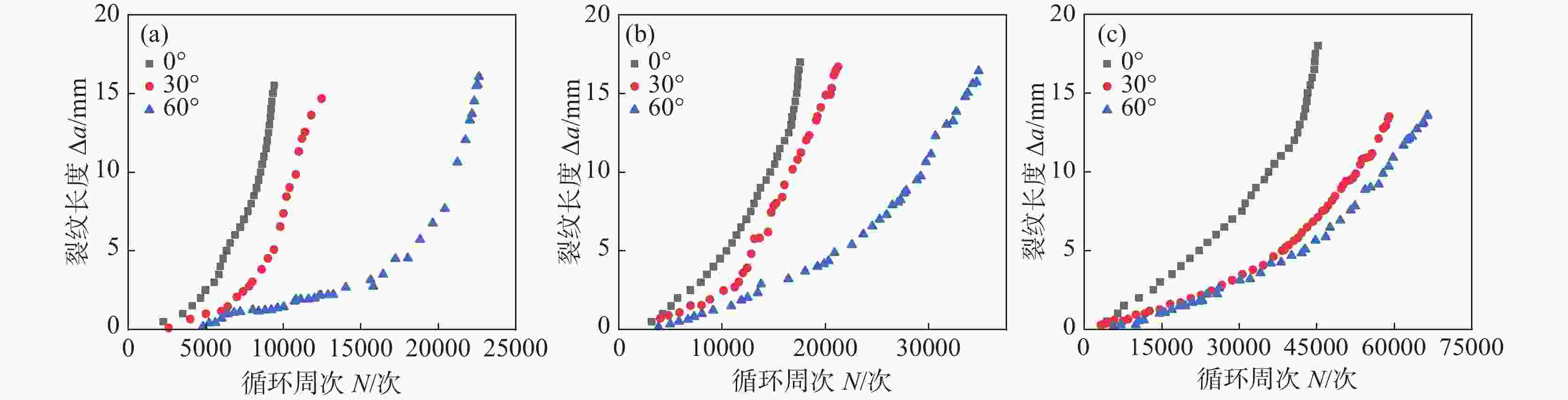
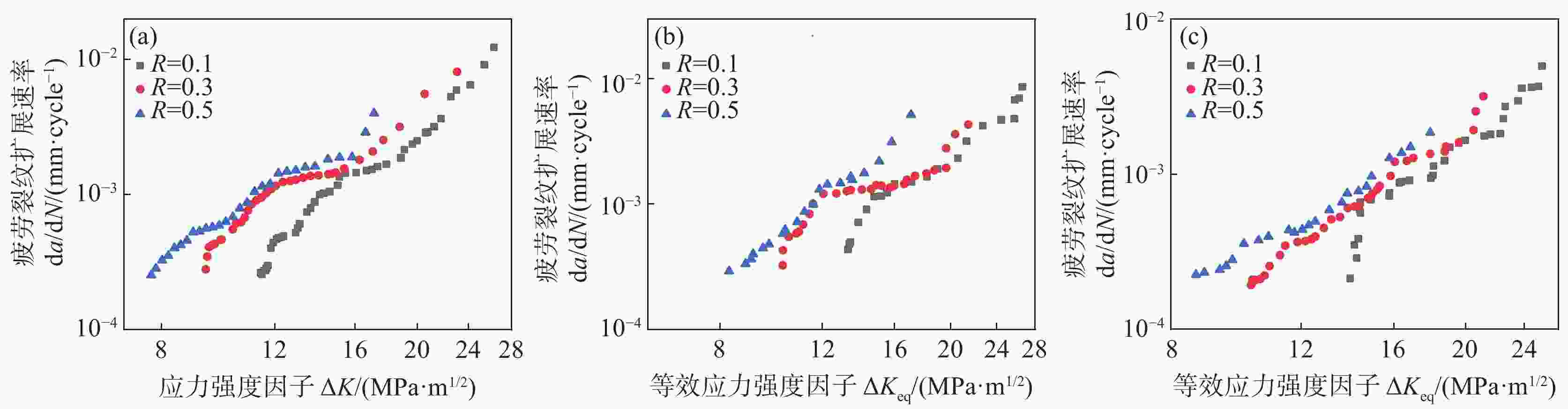
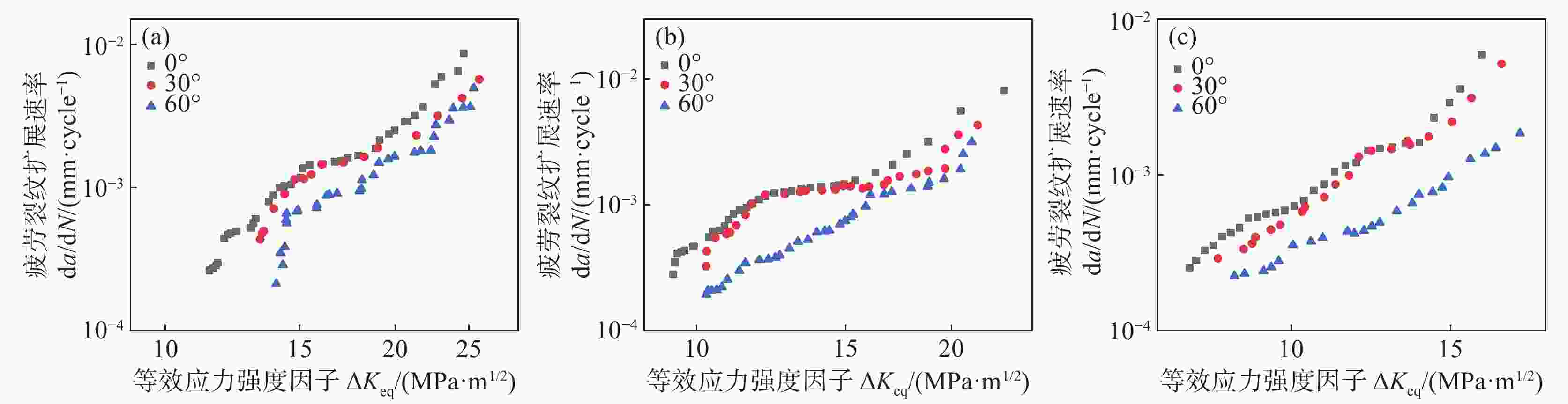
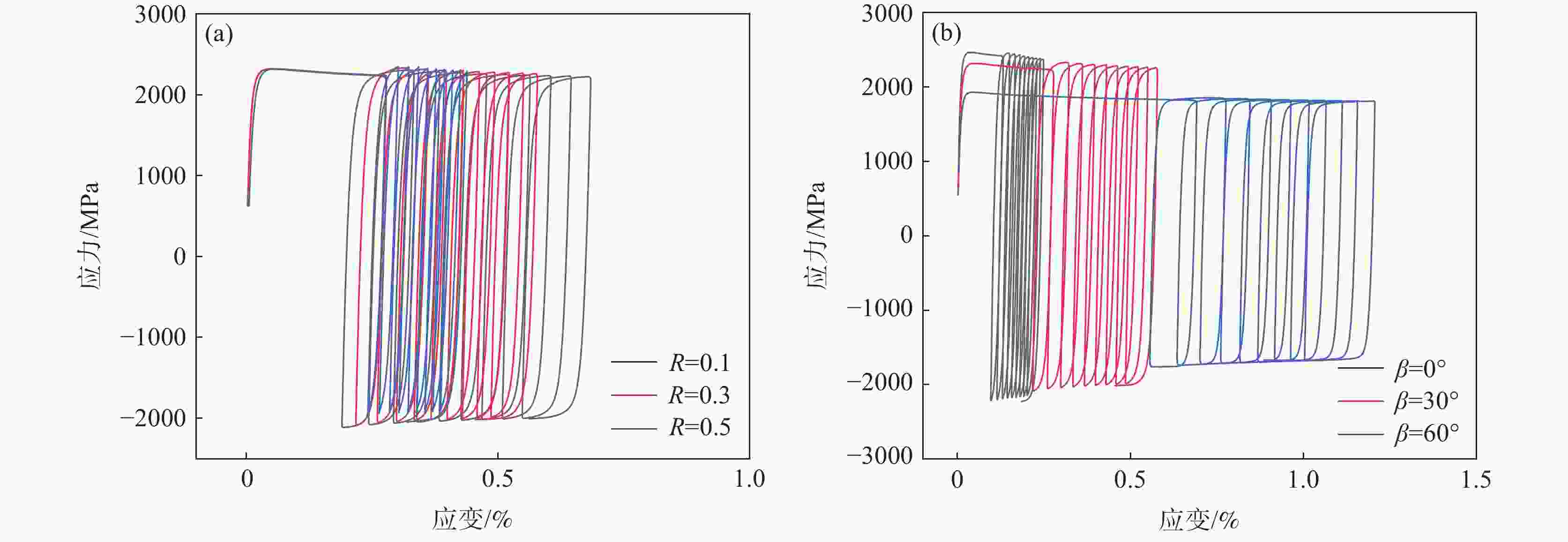
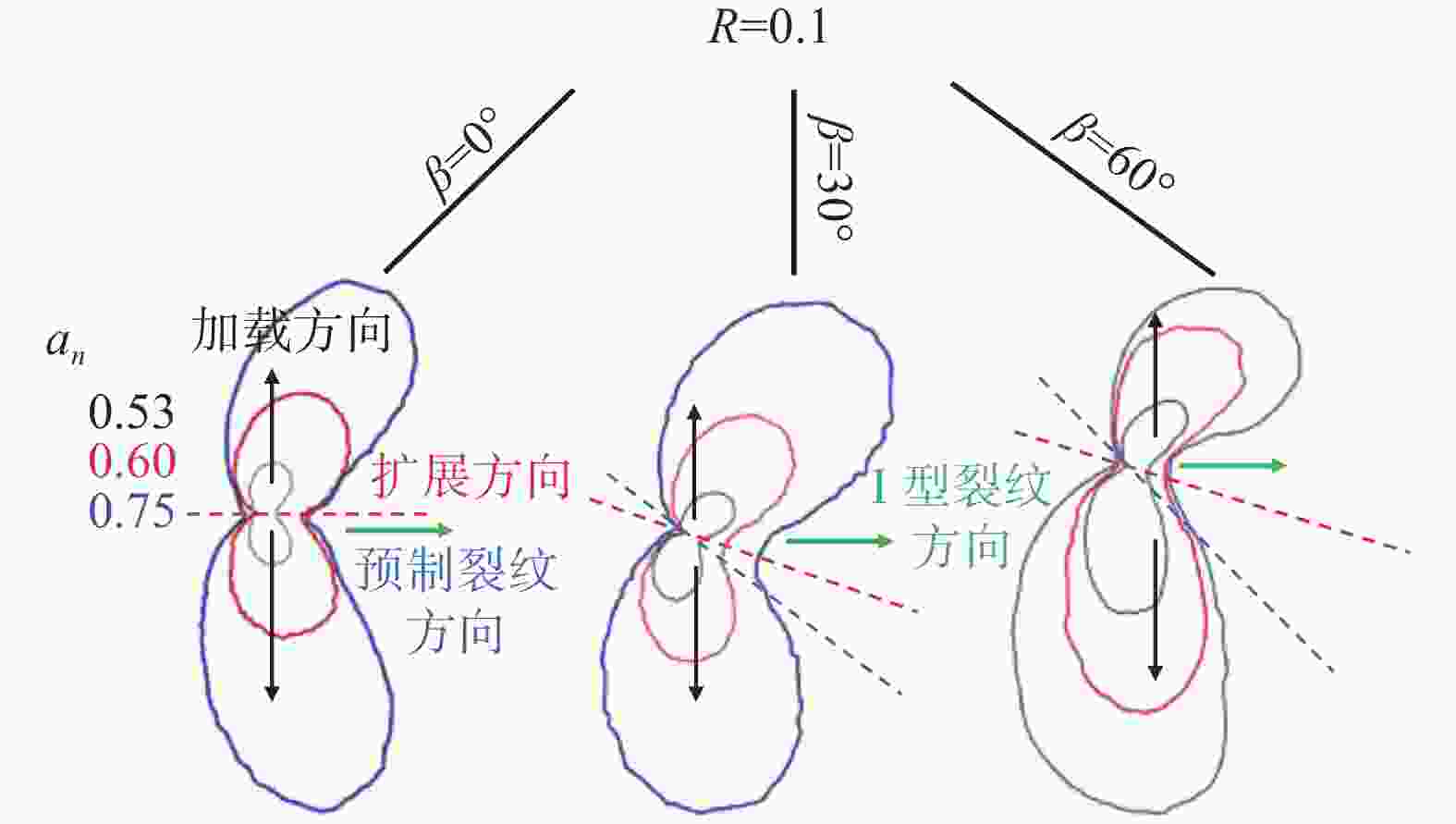
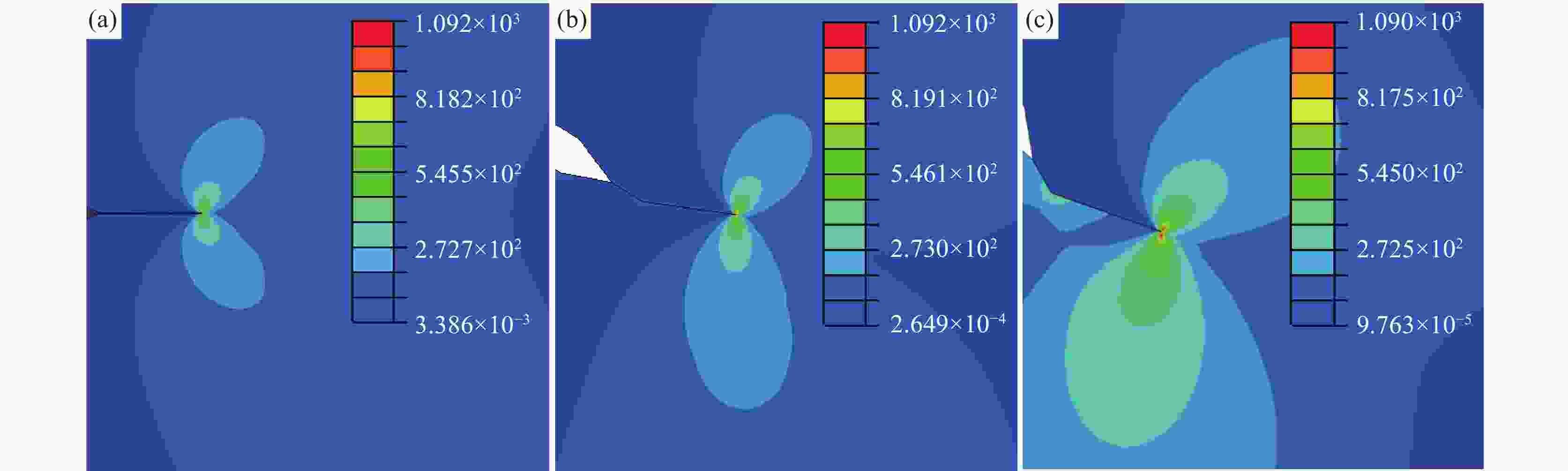
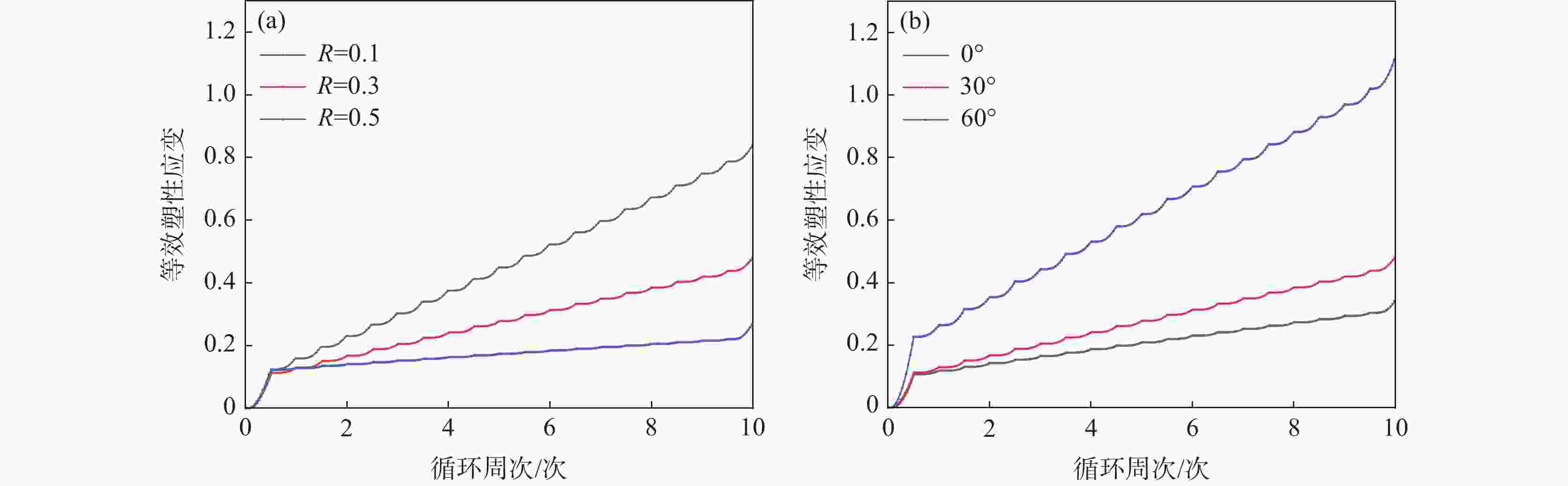
摘要: 为探究4130X钢Ⅰ-Ⅱ复合型疲劳裂纹扩展规律，采用紧凑拉伸剪切（CTS）试样，开展不同加载角度、应力比下的试验及有限元分析（FEM）。结果表明：裂纹扩展路径不受应力比R的影响，随加载角度β的增大产生较大的偏转角度，起裂扩展角符合最大周向应力（MTS）准则；疲劳裂纹扩展速率(FCGR)随应力比R的增大而增快，随着加载角度β的增加而降低；裂纹尖端的塑性区形态会随加载角度而发生变化，塑性应变能在扩展过程中逐渐累积；断口形貌特征表明，应力比R和加载角度β会对断口处的疲劳辉纹以及二次裂纹产生明显的影响。Abstract: To investigate the behavior of mixed mode I-II fatigue crack growth in 4130X steel, Compact Tension Shear (CTS) specimens were used to conduct experimental methods and Finite Element Method (FEM) at diverse load ratios and loading angles. The results indicate that the fatigue crack growth path is not influenced by the load ratio (R), but a significant deflection angle occurs with an increase in the loading angle (β). The crack growth angles are consistent with the Maximum Tangential Stress (MTS) criterion. The fatigue crack growth rate (FCGR) shows an increasing trend as load ratio (R) increases, but decreases with an increase of the loading angle (β). With the increment of the loading angle, the morphology of the monotonic plastic zone at the crack tip varies, and the plastic strain energy is accumulated gradually. Fracture morphology analysis reveals that the load ratio (R) and loading angle (β) have a significant impact on the fatigue striations and secondary cracks at the fracture surface.
-
Key words:
- 4130X steel /
- mixed mode I-II crack /
- load ratio /
- loading angle /
- fatigue crack growth rate
-
图 4 等效应力与等效塑性应变关系
Figure 4. Relationship between equivalent yield stress and equivalent plastic strain
图 6 不同应力比及加载角度下的裂纹扩展路径
Figure 6. FCG path diagram at different loading angles and load ratios
图 7 不同裂纹长度及加载角度下的应力强度因子
Figure 7. SIF at diverse loading angle under different length of crack
(a) KⅠ；(b) KⅡ
图 9 裂纹起裂角的试验值与拟合值、MTS准则预测值
Figure 9. Comparison of measured crack initiation angle with the fitting value and the predicted value by MTS criterion
图 10 不同应力比及加载角度下∆α-N曲线
Figure 10. ∆α-N curves at different loading angles and different ratios
(a)R=0.1 ；(b)R=0.3； (c)R=0.5
图 11 不同应力比下dα/dN-∆Keq关系曲线
Figure 11. dα/dN-∆Keq diagram at different load ratios
(a) β=0°；(b) β=30°；(c) β=60°
图 12 不同加载角度下dα/dN-∆Keq关系曲线
Figure 12. dα/dN-∆Keq diagram at different loading angles
(a) R=0.1；(b) R=0.3； (c) R=0.5
图 13 裂纹尖端应力-应变迟滞回线
Figure 13. Cyclic stress–strain curves at crack tip
(a) β=30°；(b) R=0.3
图 14 R=0.1下不同加载角度下裂尖单调塑性区形态及演化
Figure 14. Morphology of monotonic plastic zones under various β at R = 0.1
图 15 R=0.1下不同加载角度下Von Mises应力场演化
Figure 15. The Evolution of Von Mises stress field at different loading angles of R=0.1
(a) β=0°；(b) β=30°；(c) β=60°
图 16 不同应力比及加载角度下裂尖等效塑性应变曲线
Figure 16. Equivalent plastic strain curve of crack tip under different load ratios and loading angles
(a) β=30°；(b) R=0.3
图 17 应力比R=0.1时不同加载角度下的裂纹断口形貌
Figure 17. Fracture morphology diagram under different loading angles at R=0.1
(a)0°；(b)30°；(c)60°
图 18 同一加载角度不同应力比下裂纹断口形貌
Figure 18. Fracture morphology diagram under different load ratios at the same loading angle
(a) R=0.1, β=0°；(b) R=0.5, β=0°；(c) R=0.1, β=60°；(d) R=0.5, β=60°
表 1 4130X钢化学成分
Table 1. Chemical composition of 4130X steel
% C Mn Si Cr Mo S P Ni Cu 0.345 0.8775 0.35275 0.9975 0.1655 0.000975 0.0094 0.018 0.024 
下载: 导出CSV
表 2 4130X钢Ⅰ-Ⅱ复合型疲劳裂纹扩展试验方案
Table 2. FCG of 4130X steel for mixed mode Ⅰ-Ⅱ loading test program
NO. 加载角度β/（°） 最大载荷Pmax/kN 应力比R 1 0 3.67 0.1 2 0.3 3 0.5 4 30 0.1 5 0.3 6 0.5 7 60 0.1 8 0.3 9 0.5
下载: 导出CSV
表 3 应力强度因子解的比较
Table 3. Comparison of solutions for stress intensity factors
加载角度β/(°) 文献解[17]/
(MPa·m1/2)本文有限元解/
(MPa·m1/2)相对误差/% KⅠ KⅡ KⅠ KⅡ KⅠ KⅡ 0 26.08 0 25.91 0 0.65 0 30 26.60 −5.36 26.21 −5.44 −1.46 1.49 60 28.91 −17.81 28.41 −18.19 −1.72 2.1
下载: 导出CSV
表 4 4130X钢Chaboche模型的材料性质
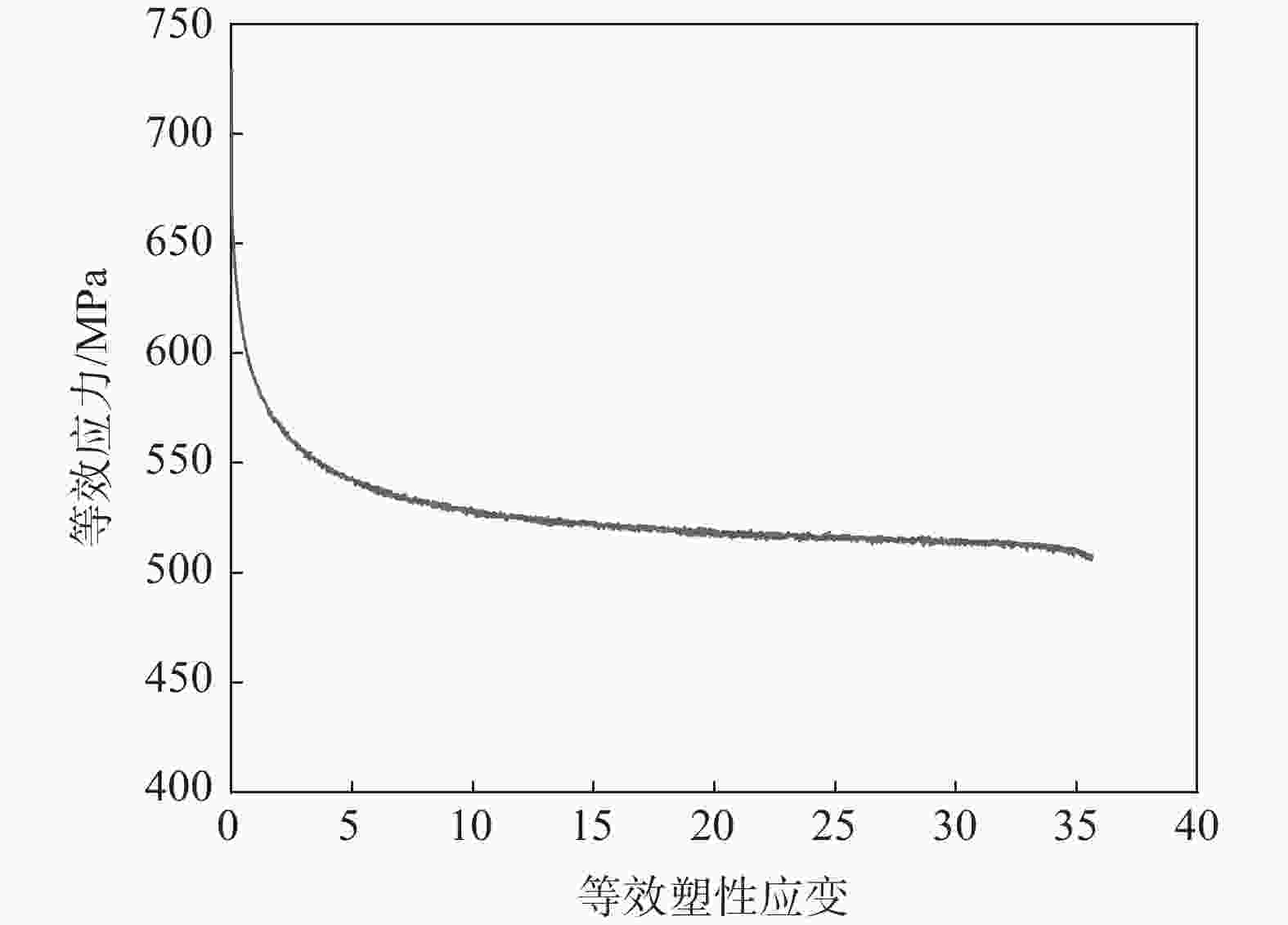
Table 4. Material properties of 4130X steel for Chaboche model
Σs/MPa σ0/MPa C1/MPa γ1 C2/MPa γ2 715 650 162000 1800 80500 230
下载: 导出CSV
表 5 KⅠ与KⅡ拟合结果
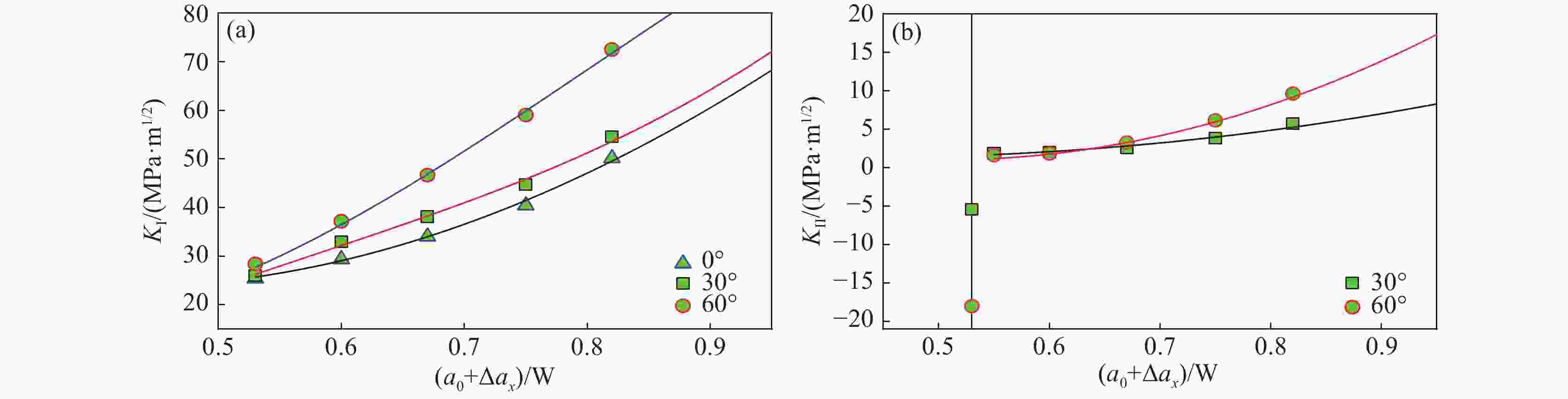
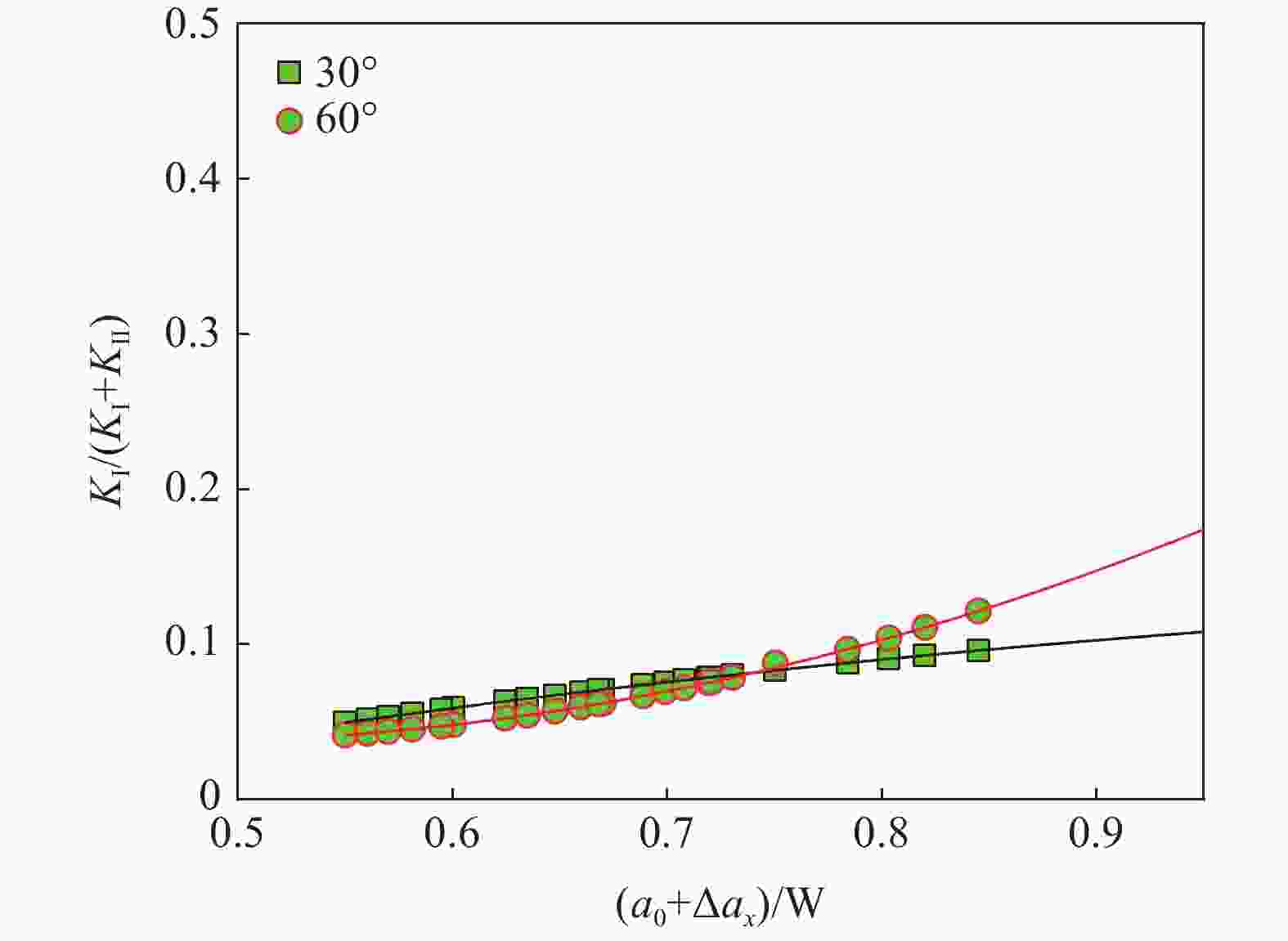
Table 5. Fitting results of KⅠ and KⅡ
β KⅠ/(MPa·m1/2) KⅡ/(MPa·m1/2) $ \mathrm{\mathit{K}}=\dfrac{\mathit{\mathrm{\mathit{F}}}}{\mathrm{\mathit{BW}}^{1/2}}\cdot f\left(a_n\right),\quad\mathit{\mathit{\mathrm{\mathit{a}}}\mathit{_{\mathrm{\mathit{n}}}}}=\left(\mathrm{\mathit{a}}_0+\Delta\mathrm{\mathit{a}}\mathit{_{\mathrm{\mathit{x}}}}\right)/\mathrm{\mathit{W}} $ $ \mathrm{\mathit{K}}=\dfrac{\mathrm{\mathit{F}}}{\mathrm{\mathit{BW}}^{1/2}}\cdot f\left(a_n\right),\quad\mathrm{\mathit{a}}\mathit{\mathit{\mathit{\mathit{_{\mathrm{\mathit{n}}}}}}}=\left(\mathrm{\mathit{a}}_0+\Delta\mathrm{\mathit{a}}_{\mathrm{\mathit{x}}}\right)/\mathrm{\mathit{W}} $ 0° $K=\dfrac{\left(2+a_n\right) \cdot \left(0.232\;84+0.431\;6\cdot a_n-1.356\;65 \cdot a_n^2+0.980\;98 \cdot a_n^3-0.287\;05 \cdot a_n^4\right)}{\left(1-a_n\right)^{1.5}} $ $ K=0 $ 30° $ f\left({a}_{n}\right)=80.043{\cdot }{a}_{n}^{3}-156.707\;6{\cdot }{a}_{n}^{2}+106.461\cdot {a}_{n}-22.738 $ $ f\left({a}_{n}\right)=-8.16\cdot {a}_{n}^{3}+20.96\cdot {a}_{n}^{2}-15.62\cdot {a}_{n}+3.79 $ 60° $ f\left({a}_{n}\right)=25.485{\cdot }{a}_{n}^{3}-42.541{\cdot }{a}_{n}^{2}+31.325\cdot {a}_{n}-6.71 $ $ f\left({a}_{n}\right)=-29.80\cdot {a}_{n}^{3}+72.18\cdot {a}_{n}^{2}-54.53\cdot {a}_{n}+13.23 $
下载: 导出CSV
表 6 不同加载角度下θ表达式
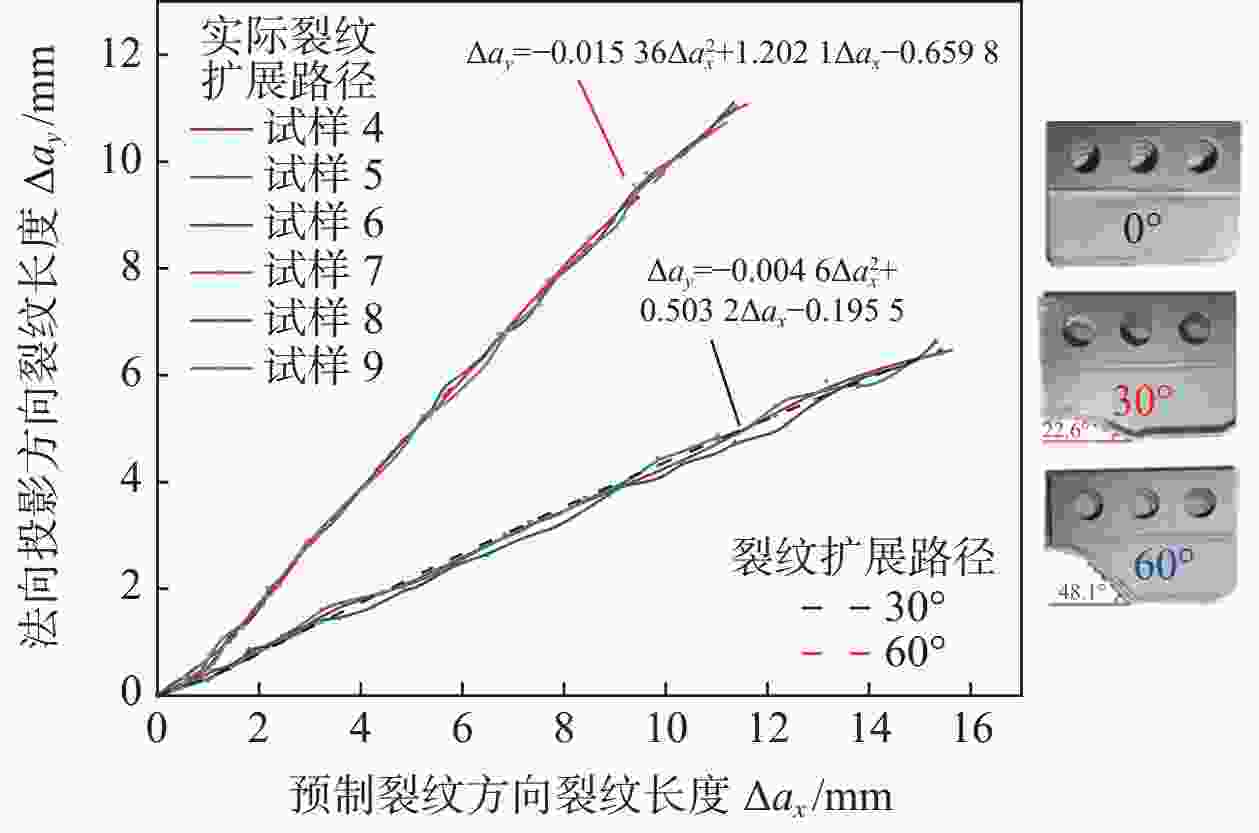
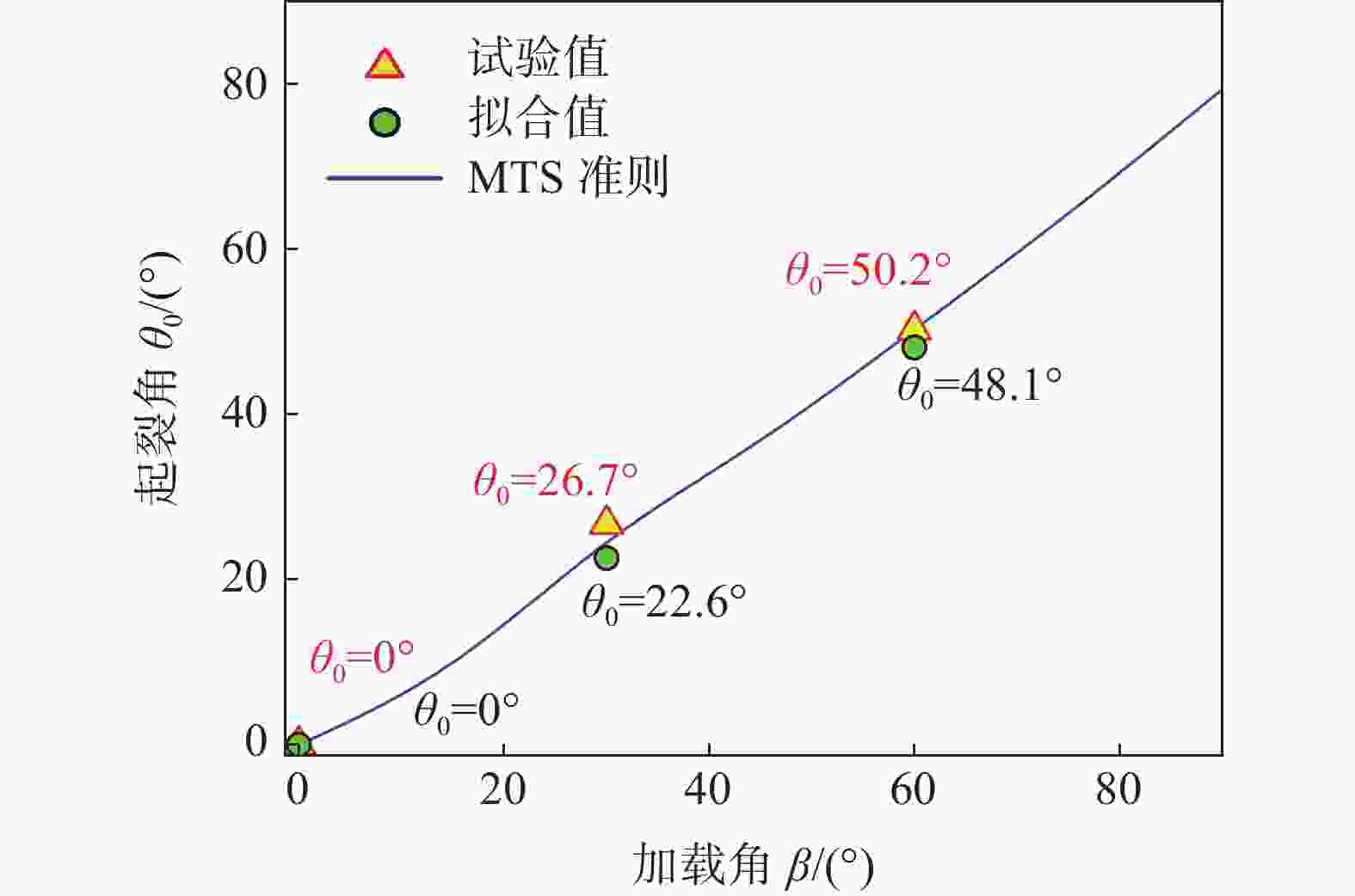
Table 6. Expression for θ under different loading angles
加载角 β/(°) θ/(°) 30 θ=arctan(− 0.0092 ×∆ax+0.5032 )60 θ =arctan(− 0.03072 ×∆ax+1.2021 )
下载: 导出CSV
-
[1] LI J, BO K, HUANG Q H, et al. Development trend and challenges of high-pressure hydrogen transportable pressure vessel[J]. Acta Energiae Solaris Sinica, 2022,43(3):20-26. (李军, 薄柯, 黄强华, 等. 高压氢气储运移动式压力容器发展趋势与挑战[J]. 太阳能学报, 2022,43(3):20-26.LI J, BO K, HUANG Q H, et al. Development trend and challenges of high-pressure hydrogen transportable pressure vessel[J]. Acta Energiae Solaris Sinica, 2022, 43（3）: 20-26. [2] NIBUR K A, MARCHI C S, SOMERDAY B P. Fracture and fatigue tolerant steel pressure vessels for gaseous hydrogen. In: ASME PVP, 2010: 18-22. [3] DING F, ZHAO T W, JIANG Y. A study of fatigue crack growth with changing loading direction[J]. Engineering Fracture Mechanics, 2006,74(13):2014-2029. [4] LUO P F, WANG C H. An experimental study on the elastic-plastic fracture in aductile material under mixed-mode loading[J]. Strain, 2008,44(3):8. [5] LIU X G, ZHU X L, GUO H D. Experimental and simulation study on Ⅰ-Ⅱ mixed-mode fatigue crack growth of TC4-DTelded joint[J]. Journal of Aeronautical Materials, 2020,40(2):61-69. (刘小刚, 朱笑林, 郭海丁. TC4-DT焊接接头Ⅰ-Ⅱ复合型疲劳裂纹扩展实验及模拟研究[J]. 航空材料学报, 2020,40(2):61-69.LIU X G, ZHU X L, GUO H D. Experimental and simulation study on Ⅰ-Ⅱ mixed-mode fatigue crack growth of TC4-DTelded joint[J]. Journal of Aeronautical Materials, 2020, 40（2）: 61-69. [6] QIAN J, FATEMI A. Mixed mode fatigue crack growth: a literature survey[J]. Engineering fracture mechanics, 1996,55(6):969-990. doi: 10.1016/S0013-7944(96)00071-9 [7] RICHARD HA, SCHRAMM B, SCHIRMEISEN N. Cracks on mixed mode loading-theories, experiments, simulations[J]. International journal of fatigue, 2014,62:93-103. doi: 10.1016/j.ijfatigue.2013.06.019 [8] SANDER M, RICHARD H. Experimental and numerical investigations on the influence of the loading direction on the fatigue crack growth[J]. Int J Fatigue, 2006,28:583-591. doi: 10.1016/j.ijfatigue.2005.05.012 [9] LIU J Y, WEN J, ZHAO J Y, et al. Fatigue crack growth behavior of CP-Ti cruciform specimens with mixed mode I-II crack under biaxial loading[J]. Materials, 2022,15(5):1926-1926. doi: 10.3390/ma15051926 [10] LI Y F, TAO H L, GAO Q, et al. Parametric simulation method for 3-D non-planar crack propagation[J]. Journal of Aerospace Power, 2017,32(12):2888-2895. (李宇飞, 陶海亮, 高庆, 等. 三维平面裂纹扩展参数化模拟方法[J]. 航空动力学报, 2017,32(12):2888-2895.LI Y F, TAO H L, GAO Q, et al. Parametric simulation method for 3-D non-planar crack propagation[J]. Journal of Aerospace Power, 2017, 32（12）: 2888-2895. [11] JIANG B, CHEN G, ZHAO H, et al. Fatigue propagation behavior of mixed mode crack in wheel steel[J]. Iron and Steel, 2018,53(12):100-104. (江波, 陈刚, 赵海. 中碳车轮钢复合型裂纹疲劳扩展行为[J]. 钢铁, 2018,53(12):100-104.JIANG B, CHEN G, ZHAO H, et al. Fatigue propagation behavior of mixed mode crack in wheel steel[J]. Iron and Steel, 2018, 53（12）: 100-104. [12] ZHAO X, NIE K, ZHU T, et al. An equivalent model of mixed-mode crack to predict the fatigue growth characteristics[J]. Chinese Journal of Solid Mechanics, 2018,39(3):296-304. (赵翔, 聂凯, 朱涛, 等. 描述复合型疲劳裂纹扩展路径的等效模型[J]. 固体力学学报, 2018,39(3):296-304.ZHAO X, NIE K, ZHU T, et al. An equivalent model of mixed-mode crack to predict the fatigue growth characteristics[J]. Chinese Journal of Solid Mechanics, 2018, 39（3）: 296-304. [13] DONG H R, GUO W L, XU F. Numerical analysis of three-dimensional Ⅰ/Ⅱ mixed-mode elastic-plastic fracture of aeronautical structural aluminum alloy[J]. Journal of Mechanical Strength, 2003, 25(2): 222-226. (董蕙茹, 郭万林, 徐绯. LC4CS铝合金三维复合型断裂的试验研究[J]. 机械强度, 2003, 25(2): 222-226.DONG H R, GUO W L, XU F. Numerical analysis of three-dimensional Ⅰ/Ⅱ mixed-mode elastic-plastic fracture of aeronautical structural aluminum alloy[J]. Journal of Mechanical Strength, 2003, 25(2): 222-226. [14] Ma S X, HU H, The mixed-mode propagation of fatigue crack in CTS specimen[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 698-704. (马世骧, 胡泓. CTS试件中复合型疲劳裂纹扩展[J]. 力学学报, 2006, 38(5): 698-704.Ma S X, HU H, The mixed-mode propagation of fatigue crack in CTS specimen[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 698-704. [15] ZHANG P, ZHOU C Y, XIE L Q, et al. Numerical investigation of mechanical behavior of crack tip under mode I and I-II mixed mode fatigue loading at negative load ratios. Theor Appl Fract Mech, 2020, 108: 102673. [16] WANG Q, LIU X, WANG W. Mixed mode fatigue crack growth behavior of Ni-Cr-Mo-V high strength steel weldments[J]. Int J Fatigue, 2017,102:79-91. doi: 10.1016/j.ijfatigue.2017.05.001 [17] ZHANG P, XIE L Q, ZHOU C Y, et al. Experimental and numerical investigation on fatigue crack growth behavior of commercial pure titanium under I-II mixed mode loading at negative load ratios[J]. Int J Fatigue, 2020,138:105700. doi: 10.1016/j.ijfatigue.2020.105700 [18] Chaboche J L. Time-independent constitutive theories for cyclic plasticity[J]. Int J Plast, 1986,2:149-188. doi: 10.1016/0749-6419(86)90010-0 [19] SONG Y Q, LI X S, LI M. Ⅰ-Ⅱ mixed-mode fatigue crack propagation of A7085 aluminum alloy and its numerical simulation[J]. Chinese Journal of Engineering, 2018,40(12):1510-1517. (宋彦琦, 李向上, 李名. A7085铝合金Ⅰ-Ⅱ复合型疲劳裂纹扩展及其数值模拟[J]. 工程科学学报, 2018,40(12):1510-1517.SONG Y Q, LI X S, LI M. Ⅰ-Ⅱ mixed-mode fatigue crack propagation of A7085 aluminum alloy and its numerical simulation[J]. Chinese Journal of Engineering, 2018, 40（12）: 1510-1517. [20] ROZUMEK D, MACHA E. A survey of failure criteria and parameters in mixed-mode fatigue crack growth[J]. Mater Sci, 2009,45:190-210. doi: 10.1007/s11003-009-9179-2 [21] SHAHANI A R, TABATABAEI S A. Effect of T-stress on the fracture of a four-point bend specimen[J]. Mater Design, 2009,30:2630-2635. doi: 10.1016/j.matdes.2008.10.031 [22] ERDOGA F. On the crack extension in plates under plane loading and transverse shear[J]. J Basic Eng Trans ASME, 1963, 85. [23] TANAKA K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis[J]. Eng Fract Mech, 1974,6:493-507. doi: 10.1016/0013-7944(74)90007-1 [24] RICARDS C E, LINDLEY T C. The influence of stress intensity and microstructure on fatigue crack propagation in ferritic materials[J] Eng Fract Mech, 1972, 4: 951-978. -
计量
- 文章访问数: 121
- HTML全文浏览量: 48
- PDF下载量: 6
- 被引次数: 0
